《安徽省2020年高考數(shù)學(xué)第二輪復(fù)習(xí) 專題升級訓(xùn)練25 解答題專項訓(xùn)練(立體幾何) 文》由會員分享，可在線閱讀，更多相關(guān)《安徽省2020年高考數(shù)學(xué)第二輪復(fù)習(xí) 專題升級訓(xùn)練25 解答題專項訓(xùn)練(立體幾何) 文（6頁珍藏版）》請在裝配圖網(wǎng)上搜索。
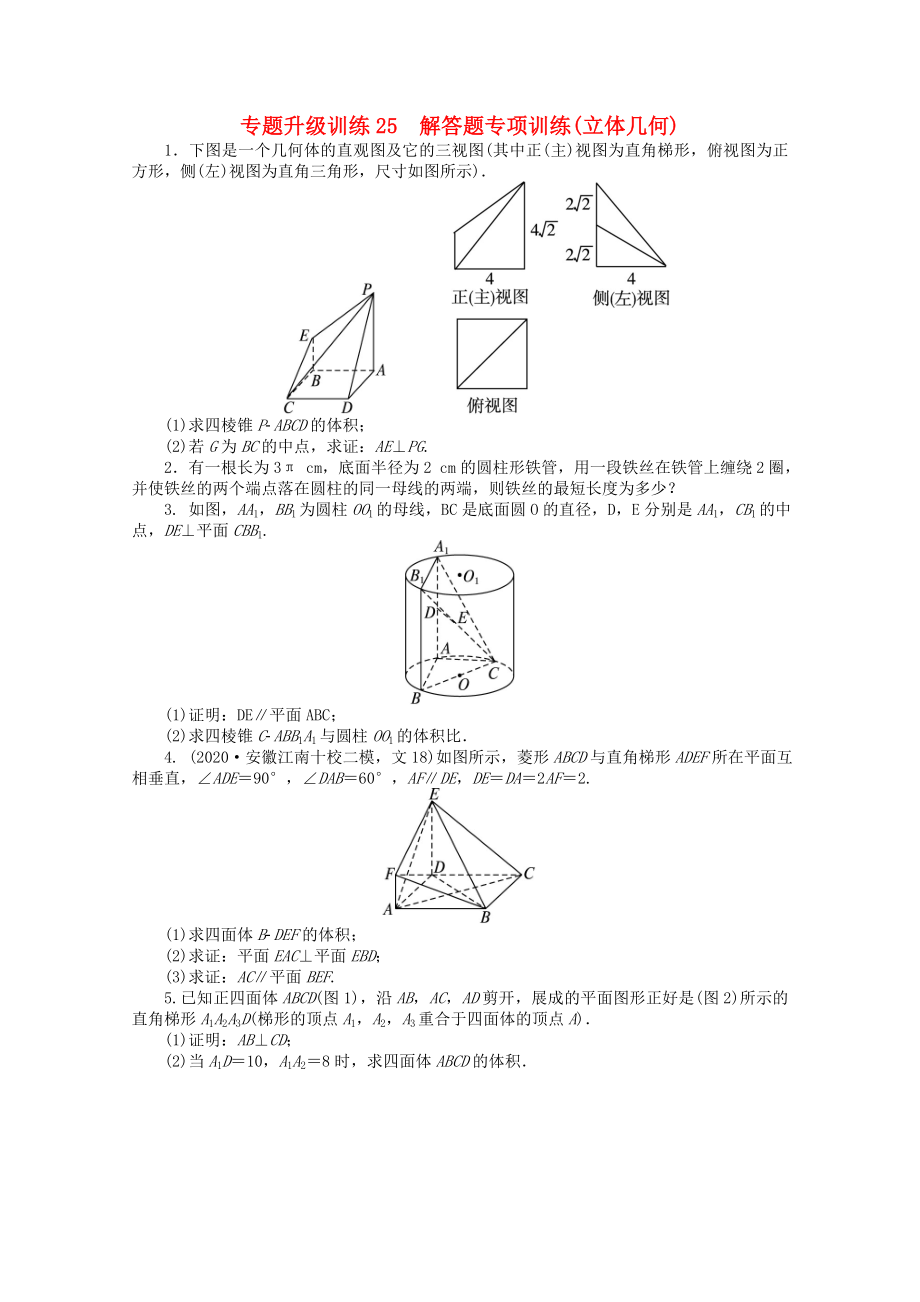
1、專題升級訓(xùn)練25解答題專項訓(xùn)練(立體幾何)1下圖是一個幾何體的直觀圖及它的三視圖(其中正(主)視圖為直角梯形，俯視圖為正方形，側(cè)(左)視圖為直角三角形，尺寸如圖所示) (1)求四棱錐PABCD的體積；(2)若G為BC的中點，求證：AEPG.2有一根長為3 cm，底面半徑為2 cm的圓柱形鐵管，用一段鐵絲在鐵管上纏繞2圈，并使鐵絲的兩個端點落在圓柱的同一母線的兩端，則鐵絲的最短長度為多少？3. 如圖，AA1，BB1為圓柱OO1的母線，BC是底面圓O的直徑，D，E分別是AA1，CB1的中點，DE平面CBB1.(1)證明：DE平面ABC；(2)求四棱錐CABB1A1與圓柱OO1的體積比4. (202
2、0安徽江南十校二模，文18)如圖所示，菱形ABCD與直角梯形ADEF所在平面互相垂直，ADE90，DAB60，AFDE，DEDA2AF2.(1)求四面體BDEF的體積；(2)求證：平面EAC平面EBD；(3)求證：AC平面BEF.5.已知正四面體ABCD(圖1)，沿AB，AC，AD剪開，展成的平面圖形正好是(圖2)所示的直角梯形A1A2A3D(梯形的頂點A1，A2，A3重合于四面體的頂點A)(1)證明：ABCD；(2)當(dāng)A1D10，A1A28時，求四面體ABCD的體積6. 如圖，已知三棱錐PABC中，PA平面ABC，ABAC，PA=AC=AB，N為AB上一點，AB=4AN，M，D，S分別為PB
3、，AB，BC的中點求證：(1)PA平面CDM；(2)SN平面CDM.7. 如圖，在三棱柱ABCA1B1C1中，側(cè)棱與底面垂直，ABC=90，AB=BC=BB1=2，M，N分別是AB，A1C的中點(1)求證：MN平面BCC1B1；(2)求證：MN平面A1B1C；(3)求三棱錐MA1B1C的體積8(2020合肥市第三次質(zhì)檢，文18)在菱形ABCD中，AC2，BD4，AC與BD交于O，將ACD沿著AC折起，使D點至點D，且D點到平面ABC的距離為，如右圖所示(1)求證：ACBD；(2)E是BO的中點，過C作平面ABC的垂線l，直線l上是否存在一點F，使EF平面ADC？若存在，求出CF的長；若不存在，
4、請說明理由參考答案1解：(1)由幾何體的三視圖可知，底面ABCD是邊長為4的正方形，PA面ABCD，PAEB，且PA4，BE2，ABADCDCB4，所以VPABCDPAS正方形ABCD444.(2)證明：連接BP.因為，EBABAP90，所以EBABAP，所以PBAAEB，所以PBABAEBEABAE90，所以PBAE.由題易證BC平面APEB，所以BCAE.又因為PBBCB，所以AE平面PBC，因為PG平面PBC，所以AEPG.2解：把圓柱側(cè)面及纏繞其上的鐵絲展開，在平面上得到矩形ABCD(如圖)，由題意知BC3 cm，AB4 cm，點A與點C分別是鐵絲的起、止位置，故線段AC的長度即為鐵絲
5、的最短長度AC5(cm)，故鐵絲的最短長度為5 cm.3(1)證明：連接EO，OA.E，O分別為B1C，BC的中點，EOBB1.又DABB1，且DA=EO=BB1.四邊形AOED是平行四邊形，即DEOA.又DE平面ABC，AO平面ABC，DE平面ABC.(2)解：由題意知DE平面CBB1，且由(1)知DEOA，AO平面CBB1，AOBC，AC=AB.因BC是底面圓O的直徑，得CAAB.而AA1CA，AA1AB=A，CA平面AA1B1B，即CA為四棱錐的高設(shè)圓柱高為h，底面半徑為r，則V柱=r2h，V錐=，V錐V柱=.4解：(1)取AD中點為G，連接BG，則BGAD，又平面ABCD平面ADEF，
6、所以BG平面ADEF.在正ABD中，BG，可求DEF的面積為2，所以四面體BDEF的體積VBDEF2.(2)證明：因為平面ABCD平面ADEF，ADE90，所以ED平面ABCD，故EDAC.又ABCD是菱形，所以BDAC.故AC平面BDE.所以平面EAC平面EBD.(3)證明：設(shè)ACBDO，取BE中點H，連接FH，OH，所以O(shè)H綉DE.又AF綉DE，所以AF綉OH，所以四邊形AFHO是平行四邊形所以AOHF，故AC平面BEF.5(1)證明：在四面體ABCD中，AB平面ACDABCD.(2)解：在題圖2中作DEA2A3于E.A1A2=8，DE=8.又A1D=A3D=10，EA3=6，A2A3=1
7、0+6=16.又A2C=A3C，A2C=8.即圖1中AC=8，AD=10，由A1A28，A1BA2B得題圖1中AB4.SACDSA3CDDEA3C8832.又AB面ACD，VBACD324.6證明：(1)在三棱錐PABC中，因為M，D分別為PB，AB的中點，所以MDPA.因為MD平面CMD，PA平面CMD，所以PA平面CMD.(2)因為M，D分別為PB，AB的中點，所以MDPA.因為PA平面ABC，所以MD平面ABC，又SN平面ABC，所以MDSN.在ABC中，連接DS，因為D，S分別為AB，BC的中點，所以DSAC且DSAC.又ABAC，所以ADSBAC90.因為ACAB，所以ACAD，所以
8、ADC45，因此CDS45.又AB4AN，所以DNADAC，即DNDS，故SNCD.又MDCDD，所以SN平面CMD.7. (1)證明：連接BC1，AC1.由題知點N在AC1上且為AC1的中點M是AB的中點，MNBC1.又MN平面BCC1B1，MN平面BCC1B1.(2)證明：三棱柱ABCA1B1C1中，側(cè)棱與底面垂直，四邊形BCC1B1是正方形，BC1B1C，MNB1C.連接A1M，由ABC=MAA1=90，BM=AM，BC=AA1得AMA1BMC.A1M=CM.又N是A1C的中點，MNA1C.B1C與A1C相交于點C，MN平面A1B1C.(3)解：由(2)知MN是三棱錐MA1B1C的高在直
9、角MNC中，MC=，NC=，MN=.又SA1B1C=，VMA1B1C=MNSA1B1C=.8解：(1)證明：設(shè)ACBDO，在菱形ABCD中，ACBD，ACOD，ACOB.又ODOBO，OD平面BOD，OB平面BOD，AC平面BOD.ACBD.(2)過D作DHDO于H，連接CH，AH，AE，CE.由(1)得平面BOD平面ABC，故HD平面ABC，故DH，所以O(shè)H1OE.四邊形AECH為平行四邊形，CHAE，CHAE.在l上截取CF，HD平面ABC，CF平面ABC，CFDH.又CFDH，四邊形CFDH為平行四邊形，CHDF，CHDF，而CHAE，CHAE，AEDF，DFAE，四邊形DAEF為平行四邊形，ADEF.又EF平面ADC，AD平面ADC，EF平面ADC，故存在F，使EF平面ADC，此時CF.
安徽省2020年高考數(shù)學(xué)第二輪復(fù)習(xí) 專題升級訓(xùn)練25 解答題專項訓(xùn)練(立體幾何) 文
