洋浦中學(xué)必修2課堂檢測——2-2-4《平面與平面平行的性質(zhì)》(教師版)

《洋浦中學(xué)必修2課堂檢測——2-2-4《平面與平面平行的性質(zhì)》(教師版)》由會員分享，可在線閱讀，更多相關(guān)《洋浦中學(xué)必修2課堂檢測——2-2-4《平面與平面平行的性質(zhì)》(教師版)（8頁珍藏版）》請在裝配圖網(wǎng)上搜索。

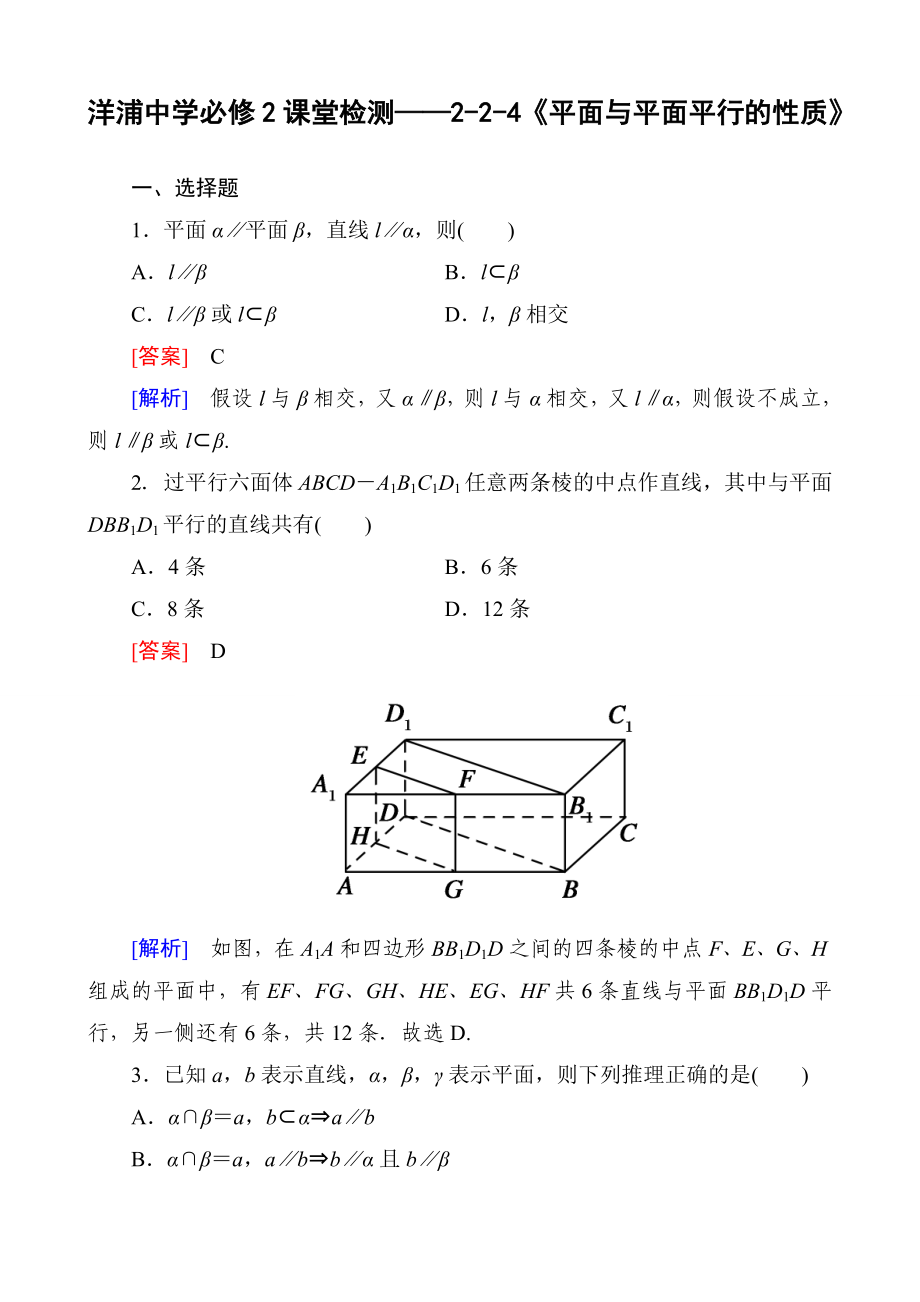
1、洋浦中學(xué)必修2課堂檢測——2-2-4《平面與平面平行的性質(zhì)》 一、選擇題 1．平面α∥平面β，直線l∥α，則(　　) A．l∥β B．l?β C．l∥β或l?β D．l，β相交 [答案]　C [解析]　假設(shè)l與β相交，又α∥β，則l與α相交，又l∥α，則假設(shè)不成立，則l∥β或l?β. 2．過平行六面體ABCD－A1B1C1D1任意兩條棱的中點作直線，其中與平面DBB1D1平行的直線共有(　　) A．4條 B．6條 C．8條 D．12條 [答案]　D [解析]　如圖，在A1A和四邊形BB1D1D之間的四條棱的中點F、E、G、H組成的平面中，有EF、FG

2、、GH、HE、EG、HF共6條直線與平面BB1D1D平行，另一側(cè)還有6條，共12條．故選D. 3．已知a，b表示直線，α，β，γ表示平面，則下列推理正確的是(　　) A．α∩β＝a，b?α?a∥b B．α∩β＝a，a∥b?b∥α且b∥β C．a(chǎn)∥β，b∥β，a?α，b?α?α∥β D．α∥β，α∩γ＝a，β∩γ＝b?a∥b [答案]　D [解析]　選項A中，α∩β＝a，b?α，則a，b可能平行也可能相交，故A不正確； 選項B中，α∩β＝a，a∥b，則可能b∥α且b∥β，也可能b在平面α或β內(nèi)，故B不正確； 選項C中，a∥β，b∥β，a?α，b?α，根據(jù)面面平行的判定定理，再加

3、上條件a∩b＝A，才能得出α∥β，故C不正確； 選項D為面面平行性質(zhì)定理的符號語言，故選D. 4．設(shè)平面α∥平面β，A∈α，B∈β，C是AB的中點，當(dāng)點A、B分別在平面α，β內(nèi)運動時，所有的動點C(　　) A．不共面 B．當(dāng)且僅當(dāng)點A、B分別在兩條直線上移動時才共面 C．當(dāng)且僅當(dāng)點A、B分別在兩條給定的異面直線上移動時才共面 D．無論點A，B如何移動都共面 [答案]　D 5．已知兩條直線m，n兩個平面α，β，給出下面四個命題： ①α∩β＝m，n?α?m∥n或者m，n相交； ②α∥β，m?α，n?β?m∥n； ③m∥n，m∥α?n∥α； ④α∩β＝m，m∥n?n∥β且n∥

4、α. 其中正確命題的序號是(　　) A．① B．①④ C．④ D．③④ [答案]　A 6．平面α∥平面β，△ABC，△A′B′C′分別在α、β內(nèi)，線段AA′，BB′，CC′共點于O，O在α、β之間．若AB＝2，AC＝1，∠BAC＝60°，OAOA′＝32，則△A′B′C′的面積為(　　) A. B. C. D. [答案]　C [解析]　如圖∵α∥β， ∴BC∥B′C′，AB∥A′B′，AC∥A′C′，∴△ABC∽△A′B′C′， 且由＝＝知相似比為， 又由AB＝2，AC＝1，∠BAC＝60°，知S△ABC＝AB·CD＝AB·(AC·sin60

5、°)＝，∴S△A′B′C′＝. 二、填空題 7．(東莞模擬)如圖是長方體被一平面所截得的幾何體，四邊形EFGH為截面，則四邊形EFGH的形狀為________． [答案]　平行四邊形 [解析]　∵平面ABFE∥平面CDHG， 又平面EFGH∩平面ABFE＝EF， 平面EFGH∩平面CDHG＝HG， ∴EF∥HG. 同理EH∥FG， ∴四邊形EFGH的形狀是平行四邊形． 8．已知平面α∥平面β，點A，C∈α，點B，D∈β，直線AB，CD交于點S，且SA＝8，SB＝9，CD＝34. (1)若點S在平面α，β之間，則SC＝________； (2)若點S不在平面α，β之間

6、，則SC＝________. [答案]　(1)16　(2)272 [解析]　(1)如圖a所示，因為AB∩CD＝S，所以AB，CD確定一個平面，設(shè)為γ，則α∩γ＝AC，β∩γ＝BD. 因為α∥β，所以AC∥BD.于是＝，即＝. 所以SC＝＝＝16. (2)如圖b所示，同理知AC∥BD，則＝， 即＝，解得SC＝272. 三、解答題 9．如圖，在四棱柱ABCD－A1B1C1D1中，底面ABCD為等腰梯形，AB∥CD，AB＝4，BC＝CD＝2，AA1＝2，E、E1分別是棱AD，AA1的中點．設(shè)F是棱AB的中點，證明：直線EE1∥平面FCC1. [證明]　因為F為AB的中點，

7、 CD＝2，AB＝4，AB∥CD， 所以CD綊AF， 因此四邊形AFCD為平行四邊形， 所以AD∥FC. 又CC1∥DD1，F(xiàn)C∩CC1＝C， FC?平面FCC1，CC1?平面FCC1， AD∩DD1＝D，AD?平面ADD1A1， DD1?平面ADD1A1， 所以平面ADD1A1∥平面FCC1. 又EE1?平面ADD1A1， EE1?平面FCC1， 所以EE1∥平面FCC1. 10．如圖，三棱柱ABC－A1B1C1中，底面是邊長為2的正三角形，點E，F(xiàn)分別是棱CC1，BB1上的點，點M是線段AC上的動點，EC＝2FB＝2.當(dāng)點M在何位置時，BM∥平面AEF? [解

8、析]　如圖，取EC的中點P，AC的中點Q，連接PQ，PB，BQ，則PQ∥AE. ∵EC＝2FB＝2，∴PE綊BF， ∴四邊形BFEP為平行四邊形， ∴PB∥EF. 又AE，EF?平面AEF，PQ，PB?平面AEF， ∴PQ∥平面AEF，PB∥平面AEF. 又PQ∩PB＝P，∴平面PBQ∥平面AEF. 又BQ?平面PBQ， ∴BQ∥平面AEF. 故點Q即為所求的點M，即點M為AC的中點時，BM∥平面AEF. 選做題．如圖，在四棱錐P－ABCD中，AB∥CD，E、F分別為PC、PD的中點，在底面ABCD內(nèi)是否存在點Q，使平面EFQ∥平面PAB？若存在，確定點Q的位置；若不存

9、在，說明理由． [解析]　取AD、BC的中點G、H，連接FG、HE. ∵F、G為DP、DA的中點，∴FG∥PA. ∵FG?平面PAB，PA?平面PAB，∴FG∥平面PAB. ∵AB∥CD，EF∥CD，∴EF∥AB. 而EF?平面PAB，AB?平面PAB，∴EF∥平面PAB. ∵EF∩FG＝F，∴平面EFG∥平面PAB. 又GH∥CD，∴GH∥EF.∴平面EFG即平面EFGH. ∴平面EFGH∥平面PAB. 又點Q∈平面ABCD， ∴點Q∈(平面EFGH∩平面ABCD)． ∴點Q∈GH.∴點Q在底面ABCD的中位線GH上． (創(chuàng)新拓展)如圖①，在直角梯形ABCP中，AP∥BC，AP⊥AB，AB＝BC＝AP，D為AP的中點，E、F、G分別為PC、PD、CB的中點，將△PCD沿CD折起，得到四棱錐PABCD，如圖②. 求證：在四棱錐P-ABCD中，AP∥平面EFG. 證明　在四棱錐P-ABCD中，E，F(xiàn)分別為PC，PD的中點， ∴EF∥CD. ∵AB∥CD，∴EF∥AB. ∵EF?平面PAB，AB?平面PAB， ∴EF∥平面PAB. 同理EG∥平面PAB.又EF∩EG＝E， ∴平面EFG∥平面PAB. ∵AP?平面PAB，AP?平面EFG， ∴AP∥平面EFG.