4月杭州市重點(diǎn)高中高考數(shù)學(xué)命題比賽參賽試題4及答案

《4月杭州市重點(diǎn)高中高考數(shù)學(xué)命題比賽參賽試題4及答案》由會(huì)員分享，可在線閱讀，更多相關(guān)《4月杭州市重點(diǎn)高中高考數(shù)學(xué)命題比賽參賽試題4及答案（14頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

1、 浙江省杭州市重點(diǎn)高中2013年4月高考命題比賽高中數(shù)學(xué)參賽試題-3 2013年高考模擬試卷數(shù)學(xué)卷（理科） （考試時(shí)間120分鐘，滿分150分） 參考公式： 如果事件互斥，那么 棱柱的體積公式 如果事件相互獨(dú)立，那么 其中表示棱柱的底面積，表示棱柱的高 棱錐的體積公式 如果事件在一次試驗(yàn)中發(fā)生的概率是， 則次獨(dú)立重復(fù)試驗(yàn)中恰好發(fā)生次的概率 其中表示棱錐的底面積，表示棱錐的高 球的表面積公式 臺(tái)體的體積公式

2、 球的體積公式 其中分別表示棱臺(tái)的上、下底面積， 表示棱臺(tái)的高 其中表示球的半徑 選擇題部分（共50分） 一、選擇題：本大題共10小題，每小題5分，共50分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的. （1）（原創(chuàng)）已知為全集，都是的子集，且，則（ ） 開(kāi)始始 S=0,T=0,n=0 T>S S=S+5

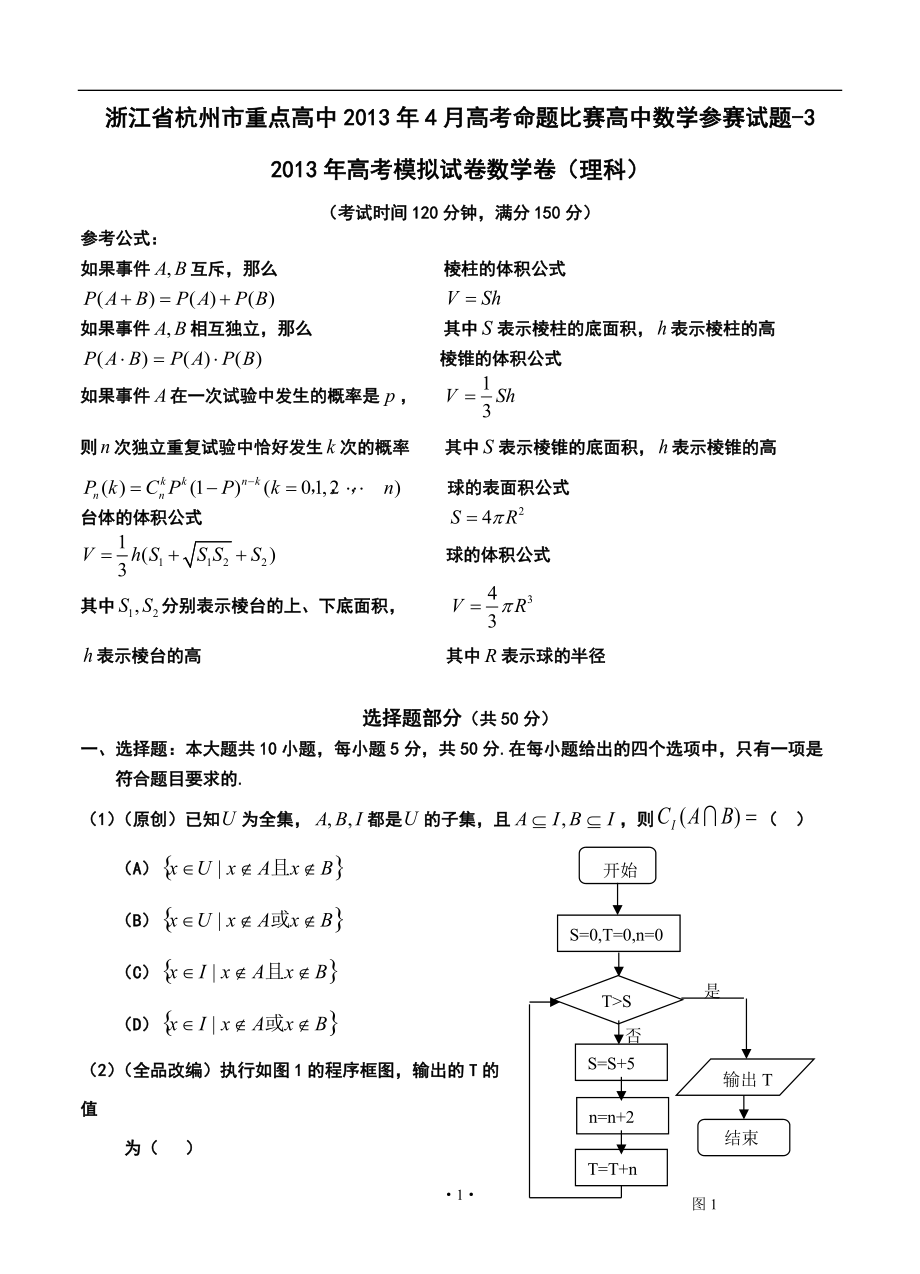
3、 n=n+2 T=T+n 輸出T 結(jié)束 是 否 圖1 （A） （B） （C） （D） （2）（全品改編）執(zhí)行如圖1的程序框圖，輸出的T的值 為（ ） （A）12 （B）20 （C）30 （D）42 （3）（原創(chuàng)）等比數(shù)列中，，則“” 　是“”的（ ） （A）充分而不必要條件 （B）必要而不充分條件 （C）充要

4、條件 （D）既不充分也不必要條件 （4）（課本改編）設(shè)為虛數(shù)單位，則下列運(yùn)算結(jié)果不是純虛數(shù)的是（ ） （A） （B） （C） （D） （5）（原創(chuàng)）已知是平面的一條斜線，點(diǎn)，為過(guò)點(diǎn)的一條動(dòng)直線，那么下列情形可能出現(xiàn)的是（ ） （A） （B） （C） （D） （6）（2007模擬題改編）已知點(diǎn)、，則直線 的傾斜角等于（ ） （A） （B） （C） （D） （7）（原創(chuàng)） 已知三頂點(diǎn)坐標(biāo)分別是、、， 直線與線段、都有公共點(diǎn)，則對(duì)于下列敘述正確的是 （ ） （

5、A）有最大值而無(wú)最小值 （B）有最小值而無(wú)最大值 圖2 （C）既有最大值也有最小值 （D）既無(wú)最大值也無(wú)最小值 （8）（原創(chuàng)）如圖2，正方體中， 為邊的中點(diǎn)，點(diǎn)在底面和側(cè)面 上運(yùn)動(dòng)并且使，那么點(diǎn) 的軌跡是（ ） （A）兩段圓弧 （B）兩段橢圓弧 （C）兩段雙曲線弧 （D）兩段拋物線弧 （9）（2011模擬題改編）中，內(nèi)角所對(duì)邊長(zhǎng)為，滿足， 如果，那么的面積等于（ ） （A） （B） （C） （D）以上都不對(duì) （10）（2011模

6、擬題改編）已知是定義在上的函數(shù)，其圖象是一條連續(xù)的曲線，且滿足下列條件：的值域?yàn)?，且；?duì)任意都有．那么，關(guān)于的方程在區(qū)間上根的情況是（ ） （A）可能沒(méi)有實(shí)數(shù)根 （B）有且僅有一個(gè)實(shí)數(shù)根 （C）恰有兩個(gè)實(shí)數(shù)根 （D）可能有無(wú)數(shù)多個(gè)實(shí)數(shù)根 非選擇題部分（共100分） 二、填空題：本大題共7小題，每小題4分，共28分． （11）（課本題改編）若的展開(kāi)式中含項(xiàng)，則最小自然數(shù)． 圖3 （12）（2012北京高考題改編）如圖3, 與都是等腰直角三角形, 且, , 平面 平面, 如果以平面為水平面, 正視圖的觀察方向與垂直,

7、 則三棱錐左視圖的面積為_(kāi)_________. （13）（2011模擬題改編）編號(hào)為1 ~8的八個(gè)小球按編號(hào)從小到大順序排成一排，涂上紅、 白兩種顏色，5個(gè)涂紅色，三個(gè)涂白色，求恰好有三個(gè)連續(xù)的小球涂紅色，則涂法共有 ______種． （14）（原創(chuàng)）首項(xiàng)的等差數(shù)列，其前項(xiàng)和為，對(duì)于一切，總有 成立，則． （15）（全品改編）已知雙曲線的左右焦點(diǎn)分別為，定點(diǎn)，點(diǎn)在雙曲線的右支上運(yùn)動(dòng)，則的最小值等于________． 圖4 （16）（2011溫州模擬題）如圖4，線段長(zhǎng)度為，點(diǎn) 分別在非負(fù)半軸和非負(fù)半軸上滑動(dòng)，以線段為 一邊，在第一象限內(nèi)作矩形，，為坐 標(biāo)原點(diǎn)，則的取值范

8、圍是 . （17）（原創(chuàng)）實(shí)數(shù)且，，則的取值范圍為_(kāi)_______． 三、解答題：本大題共5小題，共72分，解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟． （18）（2012杭州高三期中聯(lián)考改編）（本題滿分14分） 平面直角坐標(biāo)系中，滿足，， （Ⅰ）若邊長(zhǎng)等于1，求的值（只需寫(xiě)出內(nèi)的值）； （Ⅱ）若恰好等于內(nèi)角，求此時(shí)內(nèi)角的大?。? （19）（2010高考模擬改編）（本題滿分14分） 某種鮮花進(jìn)價(jià)每束元，售價(jià)每束元，若賣不出，則以每束元的價(jià)格處 理掉．某節(jié)日需求量（單位：束）的分布列為 200 300 400 500

9、 （Ⅰ）若進(jìn)鮮花束，求利潤(rùn)的均值． （Ⅱ）試問(wèn)：進(jìn)多少束花可使利潤(rùn)的均值最大？ （20）（原創(chuàng)）（本題滿分14分） 如圖5，的三邊長(zhǎng)分別為、、，為其內(nèi)心；取、 、的中點(diǎn)、、，并按虛線剪拼成一個(gè)直三棱柱（如 圖6），上下底面的內(nèi)心分別為與； 圖5 圖6 （Ⅰ）求直三棱柱的體積； （Ⅱ）直三棱柱中，設(shè)線段與平面交于點(diǎn)，求二面角 的余弦值． （21）（全品改編）（本題滿分14分） 定長(zhǎng)等于的線段的兩個(gè)端點(diǎn)分別在直線和上滑 動(dòng)，線段中點(diǎn)的軌跡為；

10、（Ⅰ）求軌跡的方程； （Ⅱ）設(shè)過(guò)點(diǎn)的直線與軌跡交于兩點(diǎn)，問(wèn)：在軸上是否存在定點(diǎn)， 使得不論如何轉(zhuǎn)動(dòng)，為定值． （22）（原創(chuàng)并將發(fā)表在數(shù)學(xué)通訊“我為高考設(shè)計(jì)題目”欄目）（本題滿分16分） 設(shè)函數(shù)，，（其中為自然底數(shù)）； （Ⅰ）求（）的最小值； （Ⅱ）探究是否存在一次函數(shù)使得且對(duì)一切恒成立；若存在，求出一次函數(shù)的表達(dá)式，若不存在，說(shuō)明理由； （Ⅲ）數(shù)列中，，，求證：． 學(xué)校 班級(jí)

11、 姓名 考號(hào) 裝 訂 線 2013年高考模擬試卷數(shù)學(xué)卷（理科） 答題卷 一、選擇題: 本大題共10小題, 每小題5分, 共50分。在每小題給出的四個(gè)選項(xiàng)中, 只有一項(xiàng)是符合題目要求的。 題 號(hào) 1 2 3 4 5 6 7 8 9 10 答案 二、填空題: 本大題共7小題, 每小題4分, 共28分。 11 ________. 12 ________. 13

12、________ .14________. 15________. 16________. 17____ ____. 三、解答題: 本大題共5小題, 共72分。解答應(yīng)寫(xiě)出文字說(shuō)明, 證明過(guò)程或演算步驟。 18、(本小題滿分14分) 19、(本小題滿分14分) 20、(本小題滿分14分)

13、 21、(本小題滿分14分) 21、(本小題滿分16分) 2013年高考模擬試卷數(shù)學(xué)卷（理科）參考答案與評(píng)分標(biāo)準(zhǔn) 一、選擇題：本大題共10小題，每小題5分，共50分. （1）D；（2）C；（3）B；（4）B；（5）A；（6）B；（7）D；（8）C （9）C

14、；（10）B 二、填空題：本大題共7小題，每小題4分，共28分． (11) 7； (12)； （13）24； （14）或； （15）11； （16）； （17） ． 三、解答題：本大題共5小題，共72分， （18）解：（Ⅰ）因?yàn)?，所以?------2分 若邊長(zhǎng)等于1，則，在內(nèi)或或----5分 由于與不共線，所以或．----------------------------7分 （Ⅱ），--10分 所以，---------------------------12分 所以．-------------------------------

15、----------------------14分 （19） 解：（Ⅰ）銷售量（單位：束）的分布列為 200 300 400 所以，-----------------------------------------------4分 而，所以．--------------7分 （Ⅱ）設(shè)進(jìn)（）束花，當(dāng)時(shí)，銷售量（單位：束）的 分布列為 200 300 400 可得；而； 同理可對(duì)其它區(qū)間討論后得 ；-------------------------11分 易知，時(shí)，取最大值．----

16、--------------------------14分 （20）解：（Ⅰ）易知為直角三角形，且其內(nèi)切圓 半徑等于2，--------1分 所以直三棱柱的高等于1，-----------------------------2分 體積； ---------------------------------------5分 圖7 （Ⅱ）如圖7以為原點(diǎn)建立空間直角坐標(biāo)系，則 ，，設(shè)平面 的法向量，則， 所以--------------------7分 再設(shè)，則由得 ；即；----------

17、-------------------------------10分 而，所以若設(shè)平面的法向量，則 ，可得；-------------------------------12分 所以，而二面角為鈍角， 所以其余弦值等于．---------------------------------------------14分 （21）解：（Ⅰ）設(shè)， 則、；--------------------------------2分 代入得軌跡的方程為 ，即；-----------------------------5分 （Ⅱ）（1）若不與軸重合，設(shè)

18、直線方程為，代入橢圓的方程得 ，設(shè)， 則，；---------------------7分 設(shè)點(diǎn)，則 ------10分 使為定值，則 ，解得 即對(duì)于點(diǎn)總有；----------------------12分 （2）當(dāng)與軸重合時(shí)，，對(duì)于點(diǎn)也有， 故在軸上存在定點(diǎn)使得為定值．---------------14分 （22）解：（Ⅰ）時(shí)，易知時(shí)、時(shí)；所以時(shí)求取最小值等于0；--

19、-----------4分 （Ⅱ）由題Ⅰ易知，，所以；----------------6分 所以可設(shè)，代入得 恒成立，所以，所以，；--------------8分 此時(shí)設(shè)，則， 易知，即對(duì)一切恒成立； 綜上，存在符合題目要求，它恰好是圖象的公切線． （如圖8所示）---------------------------------------------10分 圖8 （Ⅲ）先證遞減且； 由題（Ⅱ）知，所以 ，即為遞減數(shù)列； 又，，所以 ，… 因?yàn)楫?dāng)時(shí)總有， 所以；------------------------------13分 所以 ．-------------------------------------16分 14