《高考數(shù)學(xué)復(fù)習(xí) 課時(shí)規(guī)范練11 函數(shù)的圖象及其變換》由會(huì)員分享����,可在線閱讀,更多相關(guān)《高考數(shù)學(xué)復(fù)習(xí) 課時(shí)規(guī)范練11 函數(shù)的圖象及其變換(5頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索���。
1�����、
高考數(shù)學(xué)精品復(fù)習(xí)資料
2019.5
課時(shí)規(guī)范練11 函數(shù)的圖象及其變換
一�、選擇題
1.已知函數(shù)y=f(x)與函數(shù)y=lg的圖象關(guān)于直線y=x對(duì)稱,則函數(shù)y=f(x-2)的解析式為( )
A.y=10x-2-2 B.y=10x-1-2
C.y=10x-2 D.y=10x-1
答案:B
解析:∵y=lg,∴=10y.∴x=10y+1-2,∴f(x)=10x+1-2.∴f(x-2)=10x-1-2.
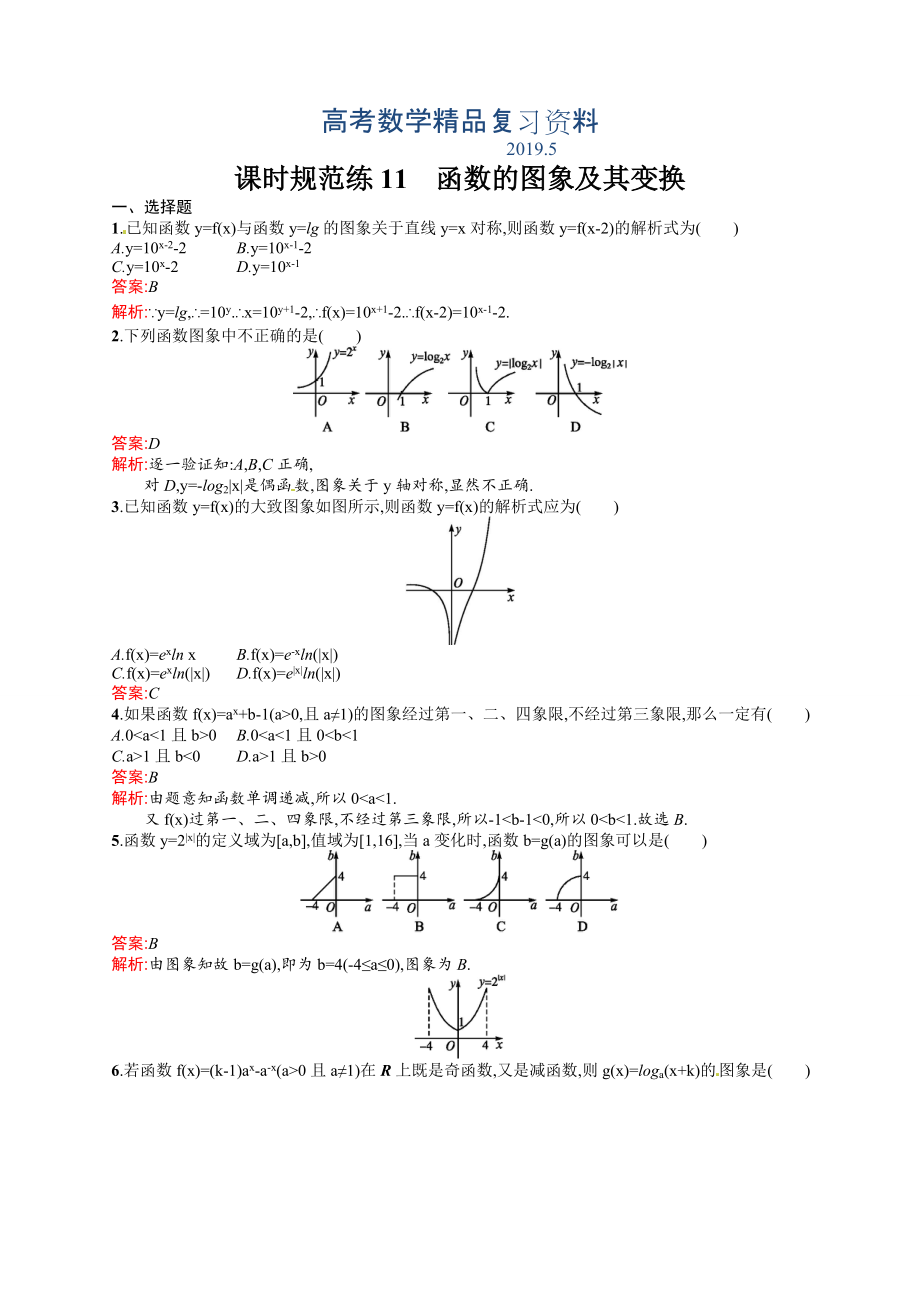
2.下列函數(shù)圖象中不正確的是( )
答案:D
解析:逐一驗(yàn)證知:A,B,C正確,
對(duì)D,y=-log2
2、|x|是偶函數(shù),圖象關(guān)于y軸對(duì)稱,顯然不正確.
3.已知函數(shù)y=f(x)的大致圖象如圖所示,則函數(shù)y=f(x)的解析式應(yīng)為( )
A.f(x)=exln x B.f(x)=e-xln(|x|)
C.f(x)=exln(|x|) D.f(x)=e|x|ln(|x|)
答案:C
4.如果函數(shù)f(x)=ax+b-1(a>0,且a≠1)的圖象經(jīng)過(guò)第一�、二、四象限,不經(jīng)過(guò)第三象限,那么一定有( )
A.00 B.01且b<0 D.a>1且b>0
答案:B
解析:由題意知函數(shù)單調(diào)遞減,所以0
3、經(jīng)過(guò)第三象限,所以-10且a≠1)在R上既是奇函數(shù),又是減函數(shù),則g(x)=loga(x+k)的圖象是( )
答案:A
解析:由函數(shù)f(x)在R上是奇函數(shù),可得f(-x)=-f(x),即(k-1)a-x-ax=(1-k)ax+a-x,∴k=2.∴f(x)=ax-a-x.
又f(x)在R上是減
4���、函數(shù),∴00)個(gè)單位,再向下平移b(b>0)個(gè)單位后圖象過(guò)坐標(biāo)原點(diǎn),則ab的值為 .
答案:1
解析:圖象平移后的函數(shù)解析式為y=-b,由題意知-b=0,∴ab=1.
9.已知函數(shù)y=的圖象與函數(shù)y=kx的圖象恰有兩個(gè)
5、交點(diǎn),則實(shí)數(shù)k的取值范圍是 .
答案:(0,1)∪(1,2)
解析:y=
函數(shù)y=kx過(guò)定點(diǎn)(0,0).
由數(shù)形結(jié)合可知:0
6����、+x)=f(1-x),所以f[1+(x+1)]=f[1-(x+1)],即f(x+2)=f(-x).故①②正確.
11.已知函數(shù)f(x)=2-x2,g(x)=x.若f(x) g(x)=min{f(x),g(x)},那么f(x) g(x)的最大值是 .(注意:min表示最小值)[來(lái)源:數(shù)理化網(wǎng)]
答案:1
解析:畫(huà)出示意圖如圖.
f(x) g(x)=
其最大值為1.
三、解答題
12.直線y=1與曲線y=x2-|x|+a有2個(gè)交點(diǎn),求a的取值范圍.
解:y=x2-|x|+a=
當(dāng)其圖象如圖所示時(shí)滿足題意.
由圖知a<1或a-=1,解得a<1或a=.
13.作出
7���、下列函數(shù)的大致圖象.
(1)y=x2-2|x|;[來(lái)源:]
(2)y=lo[3(x+2)].
解:(1)y=的圖象如圖(1).
(2)y=lo3+lo(x+2)=-1+lo(x+2)的圖象如圖(2).
14.已知函數(shù)y=f(x)同時(shí)滿足以下五個(gè)條件:
(1)f(x+1)的定義域是[-3,1];
(2)f(x)是奇函數(shù);
(3)在[-2,0)上,f(x)>0;
(4)f(-1)=0;
(5)f(x)既有最大值又有最小值.
請(qǐng)畫(huà)出函數(shù)y=f(x)的一個(gè)圖象,并寫(xiě)出相應(yīng)于這個(gè)圖象的函數(shù)解析式.
解:由(1)知,-3≤x≤1,-2≤x+1≤2,故f(x)的定義域是[-2,2
8����、].
由(3)知,f(x)在[-2,0)上是增函數(shù).
綜合(2)和(4)知,f(x)在(0,2]上也是增函數(shù),且f(-1)=f(1)=0,f(0)=0.
故函數(shù)y=f(x)的一個(gè)圖象如下圖所示,與之相應(yīng)的函數(shù)解析式是f(x)=
15.設(shè)函數(shù)f(x)=x+的圖象為C1,C1關(guān)于點(diǎn)A(2,1)對(duì)稱的圖象為C2,C2對(duì)應(yīng)的函數(shù)為g(x).
(1)求g(x)的解析式;
(2)若直線y=m與C2只有一個(gè)交點(diǎn),求m的值和交點(diǎn)坐標(biāo).
解:(1)設(shè)點(diǎn)P(x,y)是C2上的任意一點(diǎn),則P(x,y)關(guān)于點(diǎn)A(2,1)對(duì)稱的點(diǎn)為P(4-x,2-y),代入f(x)=x+,
可得2-y=4-x+,
9、
即y=x-2+.∴g(x)=x-2+.
(2)由
消去y得x2-(m+6)x+4m+9=0,
Δ=[-(m+6)]2-4(4m+9),
∵直線y=m與C2只有一個(gè)交點(diǎn),
∴Δ=0,解得m=0或m=4.
當(dāng)m=0時(shí),經(jīng)檢驗(yàn)合理,交點(diǎn)為(3,0);
當(dāng)m=4時(shí),經(jīng)檢驗(yàn)合理,交點(diǎn)為(5,4).
四�����、選做題
1.設(shè)f(x)是定義在R上的周期為3的周期函數(shù),如圖表示該函數(shù)在區(qū)間(-2,1]上的圖象,則f(2 013)+f(2 014)=( )
A.3 B.2 C.1 D.0
答案:C
解析:f(2 013)=f(3671)=f(0)=0,f(2 014)=f(3671+1
10���、)=f(1)=1,則f(2 013)+f(2 014)=1.
2.已知定義在[0,+∞)上的函數(shù)y=f(x)和y=g(x)的圖象如圖所示,則不等式f(x)g(x)>0的解集是 .
答案:
解析:由題圖可知,當(dāng)00,g(x)>0;當(dāng)0,g(x)<0;當(dāng)12時(shí),f(x)>0,g(x)>0,因此f(x)g(x)>0的解集是.
3.已知函數(shù)f(x)=m的圖象與h(x)=+2的圖象關(guān)于點(diǎn)A(0,1)對(duì)稱.
(1)求m的值;
(2)若g(x)=f(x)+在(0,2]上是減函數(shù),求實(shí)數(shù)a的取值范圍.
解:(1)設(shè)P(x,y)是h(x)圖象上一點(diǎn),點(diǎn)P關(guān)于點(diǎn)A(0,1)的對(duì)稱點(diǎn)為Q(x0,y0),
則x0=-x,y0=2-y.[來(lái)源:]
∴2-y=m,
∴y=m+2,從而m=.
(2)g(x)=.
設(shè)00,
并且在x1,x2∈(0,2]上恒成立,
∴x1x2-(a+1)<0,
∴1+a>x1x2,1+a≥4,∴a≥3.
 高考數(shù)學(xué)復(fù)習(xí) 課時(shí)規(guī)范練11 函數(shù)的圖象及其變換
高考數(shù)學(xué)復(fù)習(xí) 課時(shí)規(guī)范練11 函數(shù)的圖象及其變換