高考數(shù)學(xué) 一輪復(fù)習(xí)學(xué)案訓(xùn)練課件北師大版理科： 單元評估檢測7 第7章 立體幾何 理 北師大版

《高考數(shù)學(xué) 一輪復(fù)習(xí)學(xué)案訓(xùn)練課件北師大版理科： 單元評估檢測7 第7章 立體幾何 理 北師大版》由會員分享，可在線閱讀，更多相關(guān)《高考數(shù)學(xué) 一輪復(fù)習(xí)學(xué)案訓(xùn)練課件北師大版理科： 單元評估檢測7 第7章 立體幾何 理 北師大版（9頁珍藏版）》請在裝配圖網(wǎng)上搜索。

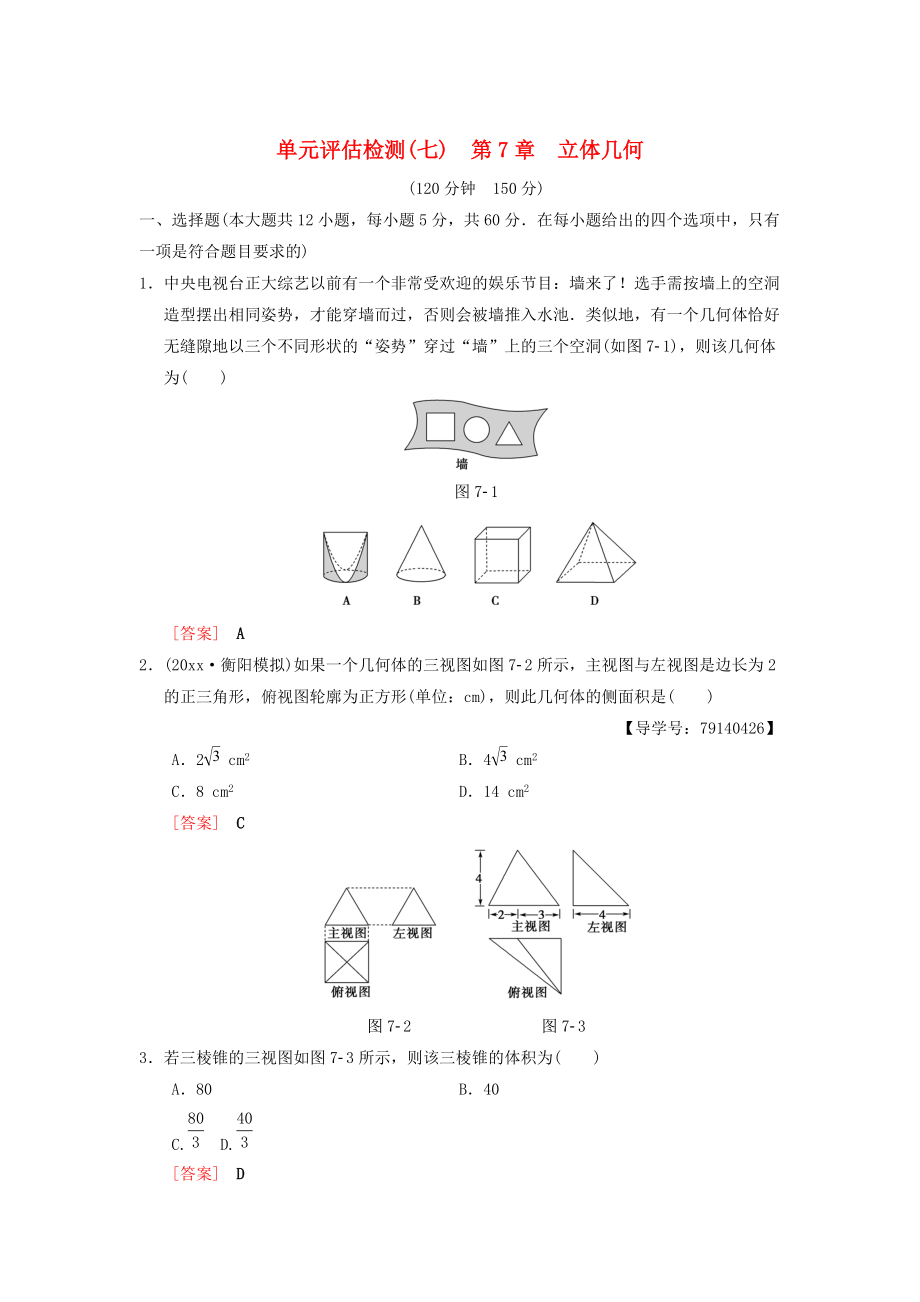
1、 單元評估檢測(七)　第7章　立體幾何 (120分鐘　150分) 一、選擇題(本大題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的) 1．中央電視臺正大綜藝以前有一個非常受歡迎的娛樂節(jié)目：墻來了！選手需按墻上的空洞造型擺出相同姿勢，才能穿墻而過，否則會被墻推入水池．類似地，有一個幾何體恰好無縫隙地以三個不同形狀的“姿勢”穿過“墻”上的三個空洞(如圖7­1)，則該幾何體為(　　) 圖7­1 [答案]　A 2．(20xx·衡陽模擬)如果一個幾何體的三視圖如圖7­2所示，主視圖與左視圖是邊長為2

2、的正三角形，俯視圖輪廓為正方形(單位：cm)，則此幾何體的側(cè)面積是(　　) 【導(dǎo)學(xué)號：79140426】 A．2 cm2 B．4 cm2 C．8 cm2 D．14 cm2 [答案]　C 　　 圖7­2　　　　　　　　圖7­3 3．若三棱錐的三視圖如圖7­3所示，則該三棱錐的體積為(　　) A．80 B．40 C. D. [答案]　D 4．(20xx·泉州模擬)設(shè)α，β是兩個不同的平面，l，m是兩條不同的直線，以下命題正確的是(　　) A．若l∥α，α∥β，則l∥β B．若l∥α，α⊥β，則l⊥β C．若l⊥α，α⊥β，則

3、l∥β D．若l⊥α，α∥β，則l⊥β [答案]　D 5．正四面體P­ABC中，D，E，F(xiàn)分別是AB，BC，CA的中點，下面四個結(jié)論中不成立的是(　　) A．BC∥平面PDF B．平面PDF⊥平面ABC C．DF⊥平面PAE D．平面PAE⊥平面ABC [答案]　B 6．在正三棱柱ABC­A1B1C1中，若AB＝2，AA1＝1，則點A到平面A1BC的距離為(　　) A. B. C. D. [答案]　B 7．如圖7­4，四面體ABCD中，AB＝DC＝1，BD＝，AD＝BC＝，二面角A­BD­C的平面角的大小為60&#

4、176;，E，F(xiàn)分別是BC，AD的中點，則異面直線EF與AC所成的角的余弦值是(　　) 圖7­4 A. B. C. D. [答案]　B 8．如圖7­5，在正方體ABCD­A1B1C1D1中，下列結(jié)論錯誤的是(　　) 圖7­5 A．直線BD1與直線B1C所成的角為 B．直線B1C與直線A1C1所成的角為 C．線段BD1在平面AB1C內(nèi)的射影是一個點 D．線段BD1恰被平面AB1C平分 [答案]　D 9．如圖7­6，在四棱錐P­ABCD中，側(cè)面PAD為正三角形，底面ABCD是邊長為2的正方形，側(cè)面PAD

5、⊥底面ABCD，M為底面ABCD內(nèi)的一個動點，且滿足MP＝MC，則點M的正方形ABCD內(nèi)的軌跡的長度為(　　) 圖7­6 A. B．2 C．π D. [答案]　A 10．棱長為4的正四面體內(nèi)切一球，然后在正四面體和該球形成的空隙處各放入一個小球，則這些小球的最大半徑為(　　) 【導(dǎo)學(xué)號：79140427】 A. B. C. D. [答案]　B 11．(20xx·南陽模擬)如圖7­7是一個由兩個半圓錐與一個長方體組合而成的幾何體的三視圖，則該幾何體的體積為(　　) 圖7­7 A．6＋ B．8＋ C．4＋ D．

6、4＋ [答案]　C 12．下列命題中錯誤的是(　　) A．如果α⊥β，那么α內(nèi)一定有直線平行于平面β B．如果α⊥β，那么α內(nèi)所有直線都垂直于平面β C．如果平面α不垂直平面β，那么α內(nèi)一定不存在直線垂直于平面β D．如果α⊥γ，β⊥γ，α∩β＝l，那么l⊥γ [答案]　B 二、填空題(本大題共4小題，每小題5分，共20分．請把正確答案填在題中橫線上) 13．半徑為的球的體積與一個長、寬分別為6,4的長方體的體積相等，則長方體的表面積為________． [答案]　88 14．(20xx·運城模擬)如圖7­8，三棱柱ABC­A1B1C1的體積

7、為V1，四棱錐A­BCC1B1的體積為V2，則＝________. 圖7­8 [答案]　 15．如圖7­9，矩形ABCD中，AB＝2AD，E為AB的中點，將△ADE沿直線DE翻折成△A1DE.若M為線段A1C的中點，則在△ADE翻折過程中，下面四個命題中正確的是________．(填序號) 圖7­9 ①BM是定值； ②點M在某個球面上運動； ③存在某個位置，使DE⊥A1C； ④存在某個位置，使MB∥平面A1DE. [答案]　①②④ 16．已知向量a＝(0，－1,1)，b＝(4,1,0)，|λa＋b|＝且λ＞0，則λ＝_____

8、___. 【導(dǎo)學(xué)號：79140428】 [答案]　3 三、解答題(本大題共6小題，共70分．解答時應(yīng)寫出必要的文字說明、證明過程或演算步驟) 17．(本小題滿分10分)(20xx·南昌模擬)如圖7­10所示，設(shè)計一個四棱錐形冷水塔塔頂，四棱錐的底面是正方形，側(cè)面是全等的等腰三角形，已知底面邊長為2 m，高為 m，則制造這個塔頂需要多少面積的鐵板？ 圖7­10 [解]　制造這個塔頂需要8 m2的鐵板． 18．(本小題滿分12分)(20xx·長沙模擬)如圖7­11，在三棱錐P­ABC中，∠PAB＝∠PAC＝∠ACB＝9

9、0°. 圖7­11 (1)求證：平面PBC⊥平面PAC； (2)若PA＝1，AB＝2，BC＝，在直線AC上是否存在一點D，使得直線BD與平面PBC所成角為30°？若存在，求出CD的長；若不存在，說明理由． [解]　(1)略　(2)存在，CD＝. 19．(本小題滿分12分)如圖7­12，在三棱柱ABC­A1B1C1中，側(cè)面ABB1A1⊥底面ABC，CA＝CB，D，E，F(xiàn)分別為AB，A1D，A1C的中點，點G在AA1上，且A1D⊥EG. 圖7­12 (1)求證：CD∥平面EFG； (2)求證：A1D⊥平面EFG.

10、 [解]　略 20．(本小題滿分12分) (20xx·江西五市三聯(lián))如圖7­13，在四棱錐P­ABCD中，AD∥BC，AB⊥AD，AB＝AD＝AP＝2BC＝2，M是棱PD上的一點，＝λ(0＜λ＜1)． 圖7­13 (1)若λ＝，求證：PB∥平面MAC； (2)若平面PAB⊥平面ABCD，平面PAD⊥平面ABCD，二面角D­AC­M的余弦值為，求λ的值． [解]　(1)略　(2). 21．(本小題滿分12分)(20xx·新鄉(xiāng)模擬)如圖7­14(1)，在三角形PCD中，AB為其中位線，且2BD＝PC，若

11、沿AB將三角形PAB折起，使∠PAD＝θ，構(gòu)成四棱錐P­ABCD，且＝＝2，如圖7­14(2)． 圖7­14 (1)求證：平面BEF⊥平面PAB； (2)當(dāng)異面直線BF與PA所成的角為60°時，求折起的角度θ. 【導(dǎo)學(xué)號：79140429】 [解]　(1)因為2BD＝PC，所以∠PDC＝90°， 因為AB∥CD，且＝＝2，所以E為CD的中點，F(xiàn)為PC的中點，CD＝2AB，所以AB∥DE且AB＝DE，所以四邊形ABED為平行四邊形，所以BE∥AD，BE＝AD， 因為BA⊥PA，BA⊥AD，且PA∩AD＝A，所以BA⊥平面PAD

12、， 因為AB∥CD，所以CD⊥平面PAD，又因為PD平面PAD，AD平面PAD， 所以CD⊥PD且CD⊥AD，又因為在平面PCD中，EF∥PD(三角形的中位線)，于是CD⊥FE. 因為在平面ABCD中，BE∥AD， 于是CD⊥BE， 因為FE∩BE＝E，F(xiàn)E平面BEF，BE平面BEF，所以CD⊥平面BEF， 又因為CD∥AB，AB在平面PAB內(nèi)，所以平面BEF⊥平面PAB. (2)因為∠PAD＝θ，取PD的中點G，連接FG，AG，所以FG∥CD，F(xiàn)G＝CD，又AB∥CD，AB＝CD， 所以FG∥AB，F(xiàn)G＝AB，從而四邊形ABFG為平行四邊形，所以BF∥AG，所以BF與PA

13、所成的角即為AG與PA所成的角，即∠PAG＝60°，因為PA＝AD，G為PD中點，所以AG⊥PD，∠APG＝30°，所以∠PDA＝30°，所以∠PAD＝180°－30°－30°＝120°.故折起的角度為120°. 22．(本小題滿分12分)(20xx·周口模擬)如圖7­15，正方形ADEF與梯形ABCD所在平面互相垂直，AD⊥CD，AB∥CD，AB＝AD＝CD＝2，點M在線段EC上且不與E，C重合． 圖7­15 (1)當(dāng)點M是EC中點時，求證：BM∥平面ADEF； (2)當(dāng)

14、平面BDM與平面ABF所成銳二面角的余弦值為時，求三棱錐M­BDE的體積． [解]　(1)取ED的中點N， 連接MN，AN， 又因為點M是EC的中點， 所以MN∥DC， MN＝DC， 而AB∥DC，AB＝DC， 所以MNAB， 所以四邊形ABMN是平行四邊形， 所以BM∥AN， 而BM?平面ADEF，AN平面ADEF， 所以BM∥平面ADEF. (2)取CD的中點O，過點O作OP⊥DM，連接BP，BO， 因為AB∥CD，AB＝CD＝2， 所以四邊形ABOD是平行四邊形， 因為AD⊥DC， 所以四邊形ABOD是矩形， 所以BO⊥CD， 因為正方形

15、ADEF與梯形ABCD所在平面互相垂直，ED⊥AD， 所以ED⊥平面ADCB， 所以平面CDE⊥平面ADCB， 所以BO⊥平面CDE，所以BP⊥DM， 所以∠OPB是平面BDM與平面DCE(即平面ABF)所成銳二面角， 因為cos∠OPB＝，所以sin∠OPB＝， 所以＝，解得BP＝. 所以O(shè)P＝BPcos∠OPB＝，所以sin∠MDC＝＝， 而sin∠ECD＝＝， 所以∠MDC＝∠ECD， 所以DM＝MC，同理DM＝EM，所以M為EC的中點， 所以S△DEM＝S△CDE＝2， 因為AD⊥CD，AD⊥DE， 且DE與CD相交于點D， 所以AD⊥平面CDE，因為AB∥CD， 所以三棱錐B­DME的高＝AD＝2， 所以VM­BDE＝VB­DEM＝S△DEM·AD＝.