《高二數(shù)學必修5 等差與等比數(shù)列基本性質(zhì)及其應(yīng)用 課件》由會員分享��,可在線閱讀�,更多相關(guān)《高二數(shù)學必修5 等差與等比數(shù)列基本性質(zhì)及其應(yīng)用 課件(18頁珍藏版)》請在裝配圖網(wǎng)上搜索。
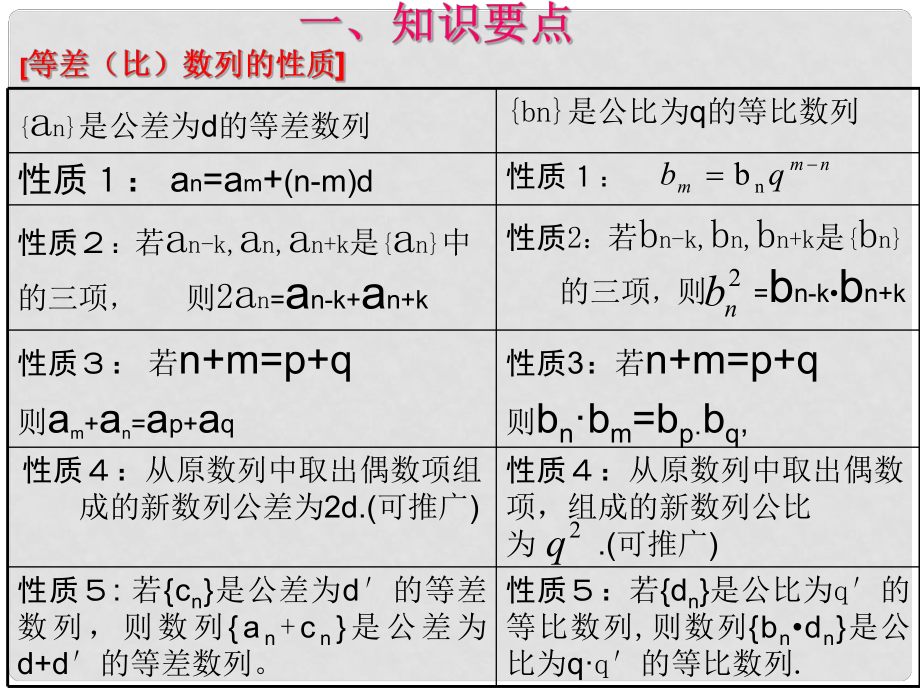
1����、an是公差為d的等差數(shù)列 bn是公比為q的等比數(shù)列 性質(zhì): an=am+(n-m)d性質(zhì): 性質(zhì):若an-k,an,an+k是an中的三項, 則2an=an-k+an+k 性質(zhì)2:若bn-k,bn,bn+k是bn的三項��,則 =bn-kbn+k性質(zhì): 若n+m=p+q則am+an=ap+aq性質(zhì)3:若n+m=p+q則bnbm=bpbq,性質(zhì):從原數(shù)列中取出偶數(shù)項組成的新數(shù)列公差為2d.(可推廣)性質(zhì):從原數(shù)列中取出偶數(shù)項��,組成的新數(shù)列公比為 .(可推廣) 性質(zhì): 若cn是公差為d的等差數(shù)列,則數(shù)列an+cn是公差為d+d的等差數(shù)列�。 性質(zhì):若dn是公比為q的等比數(shù)列,則數(shù)列bndn是公比為qq的
2、等比數(shù)列. nmmqbnb 2q2nban是公差為d的等差數(shù)列 bn是公比為q的等比數(shù)列 性質(zhì)6:數(shù)列an的前n項和為n成等差數(shù)列性質(zhì)6:數(shù)列an的前n項和為n成等比數(shù)列性質(zhì):數(shù)列an的前n項和為n性質(zhì):數(shù)列an的前n項和為n ,232nnnnnSSSSS ,232nnnnnSSSSSmnnmnSqSSmnmnndSSS 等差(比)數(shù)列的增減性:1.等差數(shù)列(前多少項和最大或最?���。ǎヾ,遞增數(shù)列����,()d,遞減數(shù)列()d����,常數(shù)列.等比數(shù)列()q,擺動數(shù)列()q�,常數(shù)列(),q���,遞減數(shù)列()��,q���,遞增數(shù)列(),q��,遞增數(shù)列()����,q,遞減數(shù)列01a01a01a01a重要性質(zhì):重要性質(zhì): am+an
3���、ap+aq(等差數(shù)列等差數(shù)列)amanapaq(等比數(shù)列等比數(shù)列)m+n=p+q(m�����、n�、p�、qN*)特別地特別地 m+n=2p時有時有: am+an2ap(等差數(shù)列等差數(shù)列) amana2p(等比數(shù)列等比數(shù)列) 返回返回特別強調(diào):特別強調(diào):已知數(shù)列 是等差數(shù)列, ���, ��。(1)求數(shù)列的通項 ��。(2)數(shù)列 的前多少項 和 最大����,最大值是多少���?(3) ��,求證:數(shù)列 是等比數(shù)列��。 na na318a 710a 2lognnab nbna.(1)設(shè)公差為d,則3117121822,22(1)2246102naadaandnaadd 得 242012nann(2)由得����,前12項和與前11項和最大,值為1
4�����、212(220)1322S11S24 22(3)log2422nnnnabnb��, 24 2(1)124 221,24nnnnnbbb數(shù)列是等比數(shù)列練習:練習:等差數(shù)列等差數(shù)列an中����,已知中,已知a 1= �,a 2 + a 5 =4a n = 33,則���,則n是(是( ) A.48 B.49 C.50 D.5131C練習練習:等比數(shù)列:等比數(shù)列an中中�����,若若a2 = 2���,a6 = 32�����, 求求a14 練習:練習:等差數(shù)列等差數(shù)列an中中, 則此數(shù)列前則此數(shù)列前20項的和等于(項的和等于( ) A.160 B.180 C.200 D.22012318192024,78aaaaaaB解:解: 2432
5、1aaa78201918aaa + 得:得:54)()()(183192201aaaaaa183192201aaaaaa54)( 3201aa18)(201aa180218*202)(2020120aas 題題1����、觀察數(shù)列:、觀察數(shù)列:30���,37��,32�,35���,34���,33,36�,( )���,38的特點,在括號內(nèi)的特點��,在括號內(nèi)適當?shù)囊粋€數(shù)是適當?shù)囊粋€數(shù)是_. 題題2���、等比數(shù)列���、等比數(shù)列an中,中�,a4+a6=3,則���,則 a5(a3+2a5+a7)=_ 題題3���、在等差數(shù)列、在等差數(shù)列an中�,若中,若a4+a6+a8+a10+a12=120,則則2a10-a12的值為的值為( ) A.20 B.22 C
6��、.24 D.28 319C練習練習題題4����、若�����、若a1��,a2�����,a3成等差數(shù)列,成等差數(shù)列����,公差為公差為d;sina1����,sina2,sina3成成等比數(shù)列����,公比為等比數(shù)列,公比為q����,則公差�,則公差d=_解解: 公差公差d= k�����,kZ 例題1��、設(shè)各項均為正數(shù)的數(shù)列an和bn滿足5an����,5bn,5an+1成等比數(shù)列�,lgbn,lgan+1��,lgbn+1成等差數(shù)列�,且a1=1,b1=2�,a2=3,求這兩個數(shù)列的通項an����,bn.能力提升為為首首項項的的等等比比數(shù)數(shù)列列以以為為公公比比是是以以2,32)2(3)2(11 aaaannn24223311 tttaatatannnn,解解得得令令得得:)(設(shè)設(shè):
7�����、233321 nnnnaa得:得: 11134 (2)nnnnaaaannNa (2)在(2)在中中,求求換元法換元法三�、歸納小結(jié)三、歸納小結(jié)本節(jié)課主要復(fù)習歸納了本節(jié)課主要復(fù)習歸納了等差等差(比比)數(shù)列的概念����、數(shù)列的概念、等差(比)數(shù)列的通項公式與前等差(比)數(shù)列的通項公式與前n項和公式��,項和公式���,以及一些相關(guān)的性質(zhì)以及一些相關(guān)的性質(zhì)1�、基本方法:掌握等差(比)數(shù)列通項公����、基本方法:掌握等差(比)數(shù)列通項公式和前式和前n項和公式�;項和公式;2���、利用性質(zhì):掌握等差(比)數(shù)列的重要���、利用性質(zhì):掌握等差(比)數(shù)列的重要性質(zhì);掌握一些比較有效的技巧����;性質(zhì)�;掌握一些比較有效的技巧����;主要內(nèi)容:主要內(nèi)容:應(yīng)
8、當掌握:應(yīng)當掌握: 題1等差數(shù)列an中�,an-m=A,an+m=B��;等比數(shù)列bn中�����,bn-m=A�����,bn+m=B�����;則有() Aan=A+B����,bn= Ban= ���,bn= Can= ,bn= Da2n=A+B���,b2n=AB2ABAB2ABABAB四����、學生課堂鞏固練習四�����、學生課堂鞏固練習:【解析】由等差�����、等比中項定義�,知選C.C題2����、已知數(shù)列an,anN*����,Sn= (an+2)2. (1)求證:an是等差數(shù)列�����; (2)若b1=1�����,b2=4�����,bn前n項和為Bn��,且Bn+1=(an+1-an+1)Bn+(an-an+1)Bn-1(n2).求bn通項公式. 18【解析】(1)an+1=Sn+1-Sn= (a
9��、n+1+2)2-(an+2)2, 8an+1=(an+1+2)2-(an+2)2, (an+1-2)2-(an+2)2=0, (an+1+an)(an+1-an-4)=0�, anN*�,an+1+an0, an+1-an-4=0��,即an+1-an=4��,18數(shù)列an是等差數(shù)列. (2)由an+1-an=4���,由題知 Bn+1=5Bn-4Bn-1����, Bn+1-Bn=4(Bn-Bn-1), bn+1=4bn(n2). 又已知b1=1����,b2=4, 故bn是首項為1��,公比為4的等比數(shù)列. bn=4n-1(nN*)題題1 在等比數(shù)列在等比數(shù)列 中�����,中��, na(1)若)若 則則485,6,aa210aa(2)若
10����、)若 則則5102,10,aa15a(4)若)若 則則1234324,36,aaaa56aa6a (3)已知)已知 求求3458,aaa23456aaaaa305032430今日作業(yè)今日作業(yè)_;,20, 8)3(_,33,39)2(_;,30,50)1(,756015963852741753 aaaaaaaaaaaaaaaan則則若若則則若若則則若若中中在等差數(shù)列在等差數(shù)列題2102724題題3、數(shù)列����、數(shù)列an與與bn的通項公式分別為的通項公式分別為an=2n���,bn=3n+2�,它們的公共項由小到大排成的數(shù),它們的公共項由小到大排成的數(shù)列是列是cn. 寫出寫出cn的前的前5項項. 證明證明cn是等比數(shù)列是等比數(shù)列.
 高二數(shù)學必修5 等差與等比數(shù)列基本性質(zhì)及其應(yīng)用 課件
高二數(shù)學必修5 等差與等比數(shù)列基本性質(zhì)及其應(yīng)用 課件