《2018年春八年級數(shù)學下冊 18.1 平行四邊形 18.1.1 平行四邊形的性質特色訓練題 （新版）新人教版》由會員分享，可在線閱讀，更多相關《2018年春八年級數(shù)學下冊 18.1 平行四邊形 18.1.1 平行四邊形的性質特色訓練題 （新版）新人教版（2頁珍藏版）》請在裝配圖網上搜索。
18.1.1 平行四邊形性質（特色訓練題）
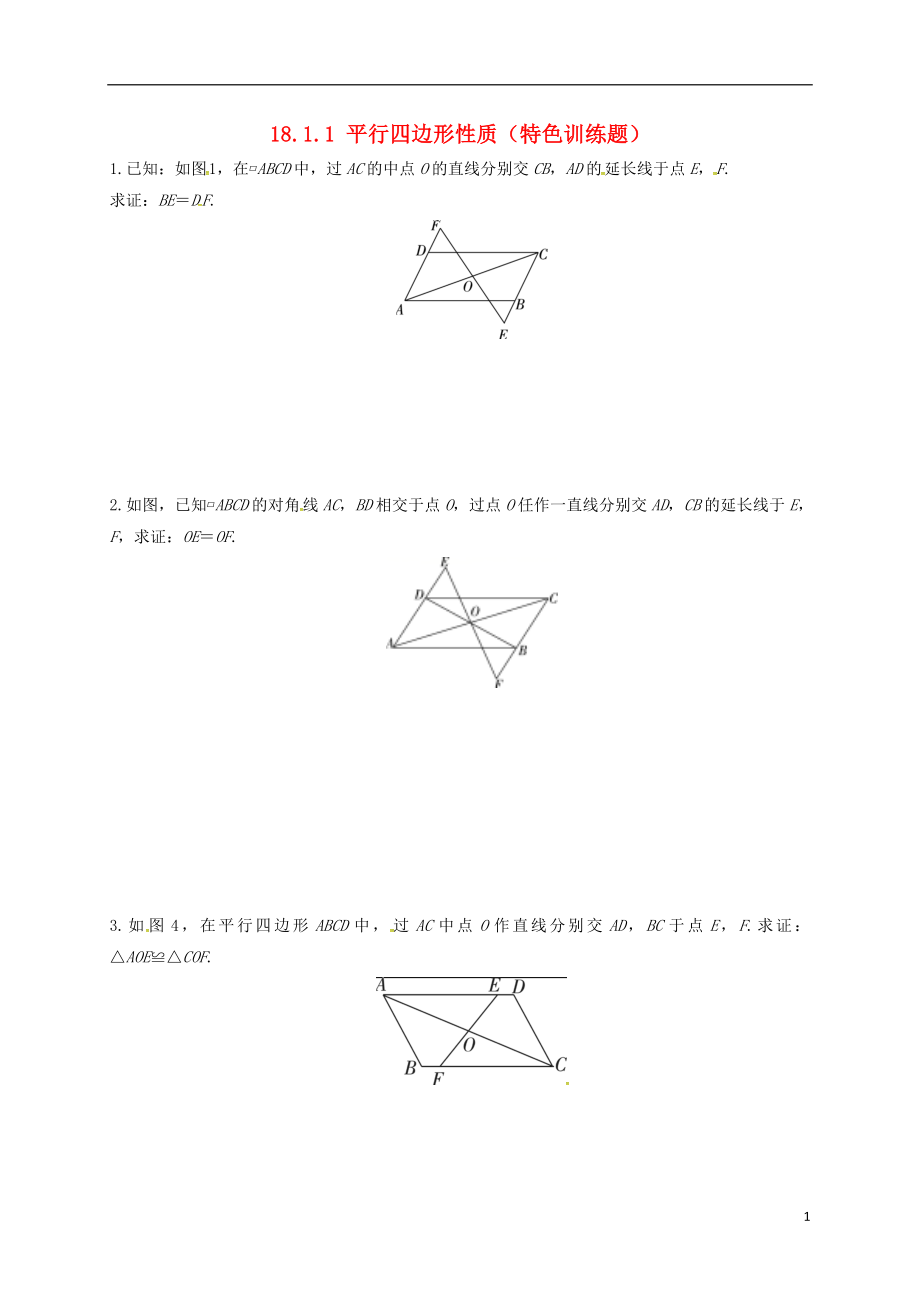
1.已知：如圖1，在?ABCD中，過AC的中點O的直線分別交CB，AD的延長線于點E，F(xiàn).
求證：BE＝DF.
2.如圖，已知?ABCD的對角線AC，BD相交于點O，過點O任作一直線分別交AD，CB的延長線于E，F(xiàn)，求證：OE＝OF.
3.如圖4，在平行四邊形ABCD中，過AC中點O作直線分別交AD，BC于點E，F(xiàn).求證：△AOE≌△COF.
參考答案
1.證明：在平行四邊形ABCD中，點O是AC的中點，
∴OA＝OC，AD∥BC，
AD＝BC，
∴∠FAC＝∠ECA，
又∠AOF＝∠COE，
∴△AOF≌△COE(ASA)，
∴AF＝CE，∴AF－AD＝CE－BC，
即DF＝BE.
2.證明：在?ABCD中，
AO＝CO，AD∥BC，
∴∠E＝∠F，
∠EAO＝∠FCO.
在△AOE和△COF中，
∴△AOE≌△COF(AAS)，
∴OE＝OF.
3.證明：∵O為AC中點，
∴OA＝OC.
∵四邊形ABCD為平行四邊形，
∴AD∥BC.
∴∠EAO＝∠FCO，
∠AEO＝∠CFO.
∴ △AOE≌△COF.
2
2018年春八年級數(shù)學下冊 18.1 平行四邊形 18.1.1 平行四邊形的性質特色訓練題 （新版）新人教版
