山東省龍口市蘭高鎮(zhèn)2018年中考數(shù)學(xué) 三角形分類訓(xùn)練三 全等三角形 魯教版

《山東省龍口市蘭高鎮(zhèn)2018年中考數(shù)學(xué) 三角形分類訓(xùn)練三 全等三角形 魯教版》由會員分享，可在線閱讀，更多相關(guān)《山東省龍口市蘭高鎮(zhèn)2018年中考數(shù)學(xué) 三角形分類訓(xùn)練三 全等三角形 魯教版（9頁珍藏版）》請在裝配圖網(wǎng)上搜索。

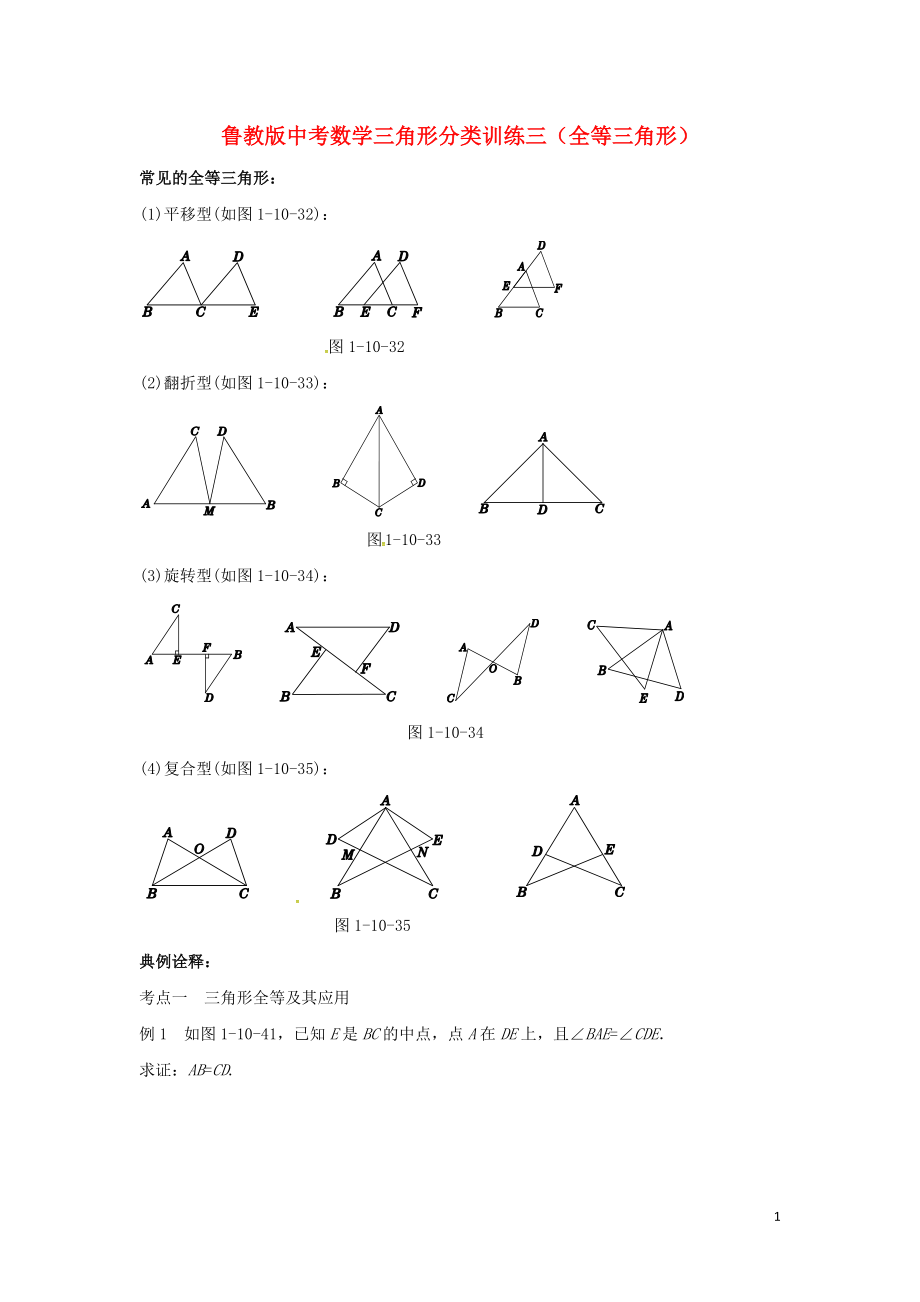
1、魯教版中考數(shù)學(xué)三角形分類訓(xùn)練三（全等三角形） 常見的全等三角形： (1)平移型(如圖1-10-32)： 圖1-10-32 (2)翻折型(如圖1-10-33)： 圖1-10-33 (3)旋轉(zhuǎn)型(如圖1-10-34)： 圖1-10-34 (4)復(fù)合型(如圖1-10-35)： 圖1-10-35 典例詮釋： 考點一 三角形全等及其應(yīng)用 例1 如圖1-10-41，已知E是BC的中點，點A在DE上，且∠BAE=∠CDE． 求證：AB=CD.

2、 圖1-10-41 【證明】 如圖1-10-42,延長DE到F，使EF=DE，連接BF .∵ E是BC的中點，∴ BE=CE. 圖1-10-42 ∵ 在△BEF和△CED中， ∴ △BEF≌△CED．∴ ∠F=∠CDE，BF=CD． ∵ ∠BAE=∠CDE，∴ ∠BAE=∠F,∴ AB=BF. 又∵ BF=CD，∴ AB=CD． 【名師點評】 此題要證明AB=CD，不能通過證明△ABE和△CED全等得到，因為根據(jù)已知條件無法證明它們?nèi)?，那么可以利用等腰三角形的性質(zhì)來解題，為此必須把AB和CD通過作輔助線轉(zhuǎn)化到一個等腰三角形中． 例2 (2016

3、·石景山一模)如圖1-10-43，已知AD=AE，請你添加一個條件 ，使得△ADC≌△AEB. 圖1-10-4 【答案】 ∠C=∠B或AC=AB等(答案不唯一) 【名師點評】 此題考查兩個三角形全等的條件，此題答案不唯一. 例3 (2016·順義一模)如圖1-10-44，已知B，A，E在同一直線上，AC∥BD且AC=BE，∠ABC=∠D．求證：AB=AD． 圖1-10-44 【證明】 ∵ AC∥BD，∴ ∠BAC=∠DBE． 在△ABC和△BDE中， ∴ △ABC≌△BDE(AAS)，∴ AB=BD． 考點二 尺規(guī)作圖 例4 (2016·房

4、山二模)閱讀下面材料：在數(shù)學(xué)課上，老師提出如下問題： 尺規(guī)作圖： 已知：Rt△ABC，∠C=90°(如圖1-10-45)． 圖1-10-45 求作：Rt△DEF，使∠DFE=90°，DE=AB，F(xiàn)E = CB． 小蕓的作圖步驟如下： 如圖1-10-46, 圖1-10-46 (1)作線段FE=CB； (2)過點F作GF⊥FE于點F； (3)以點E為圓心,AB的長為半徑作弧，交射線FG于點D，連接DE. 所以△DEF即為所求作的直角三角形． 老師說：“小蕓的作圖步驟正確，且可以得到DF=AC”． 請回答：得到DF=AC的依據(jù)是

5、 ． 【答案】 全等三角形的對應(yīng)邊相等 【名師點評】 此題考查兩個直角三角形全等的判定定理(HL)，學(xué)生要能通過閱讀作圖步驟，找到哪些是已知條件，從而找到兩個三角形全等的依據(jù). 基礎(chǔ)精練 1.(2016·通州一模)如圖1-10-47，在△ABC中，AC=BC，BD⊥AC于點D，在△ABC外作∠CAE=∠CBD，過點C作CE⊥AE于點E.如果∠BCE =140°，求∠BAC的度數(shù). 圖1-10-47 【解】 ∵ BD⊥AC，CE⊥AE，∴ ∠BDC=∠E=90°. ∵ ∠CAE=∠CBD，∴ △BDC∽△AEC，∴ ∠BCD=∠ACE. ∵ ∠B

6、CE=140°，∴ ∠BCD=∠ACE=70°. ∵ AC=BC，∴ ∠BAC=∠ABC=55°. 2.(2016·西城二模)如圖1-10-48，在△ABC中，D是AB邊上一點，且DC=DB,點E在CD的延長線上，且∠EBC=∠ACB．求證：AC=EB． 圖1-10-48 【證明】 ∵ DC=DB，∴ ∠DCB=∠DBC． 在△ACB和△EBC中，∴ △ACB≌△EBC，∴ AC=EB． 3.(2016·東城二模)如圖1-10-49，已知∠ABC=90°，分別以AB和BC為邊向外作等邊 △ABD和等邊△BCE，連接AE，CD.求證：AE=CD. 圖1-10-49

7、 【證明】 如圖1-10-49，∵ △ABD和△BCE為等邊三角形， ∴ ∠ABD=∠CBE=60°，BA=BD，BC=BE, ∴ ∠ABD+∠ABC=∠CBE+∠ABC，即∠CBD=∠ABE. 在△CBD和△EBA中， ∴ △CBD≌△EBA(SAS)，∴ AE=CD. 4.(2016·海淀二模)如圖1-10-50，在△ABC中，∠ACB=90°，點D在BC上，且BD=AC，過點D作DE⊥AB于點E，過點B作CB的垂線，交DE的延長線于點F．求證：AB=DF． 圖1-10-50 【證明】 如圖1-10-51. 圖1-10-51 ∵ BF⊥BC，DE⊥AB，∠AC

8、B=90°， ∴ ∠DBF=∠BEF=∠ACB=90°, ∴ ∠1+∠2=90°，∠2+∠F=90°. ∴ ∠1=∠F. 在△ABC和△DFB中， ∴ △ABC≌△DFB，∴ AB=DF. 5.如圖1-10-52，在△MNQ中，MQ≠NQ． 圖1-10-52 (1)請你以MN為一邊，在MN的同側(cè)構(gòu)造一個與△MNQ全等的三角形，畫出圖形，并簡要說明構(gòu)造的方法； (2)參考(1)中構(gòu)造全等三角形的方法解決下面問題： 如圖1-10-53，在四邊形ABCD中，∠ACB+∠CAD=180°，∠B=∠D．求證：CD=AB． 圖1-10-53 (1)【解】 如圖1-10-5

9、4①,過點N在MN的同側(cè)作∠MNR=∠QMN，在NR上截取NP=MQ，連接MP，則△MNP即為所求． ① ② 圖1-10-54 (2)【證明】 如圖1-10-54②，延長BC到點E，使CE=AD，連接AE． ∵ ∠ACB+∠CAD=180°，∠ACB+∠ACE=180°，∴ ∠CAD=∠ACE． 又∵ AD=CE，AC=CA，∴ △ACD≌△CAE．∴ ∠D=∠E，CD=AE． ∵ ∠B=∠D，∴ ∠B=∠E，∴ AE=AB，∴ CD=AB． 6.(2014·河南)(1)問題發(fā)現(xiàn) 如圖1-10-55，△ACB和△DCE均為等邊三角形

10、，點A，D，E在同一直線上，連接BE. 填空：①∠AEB的度數(shù)為 ； 圖1-10-55 ②線段AD,BE之間的數(shù)量關(guān)系是 ． (2)拓展探究 如圖1-10-56，△ACB和△DCE均為等腰直角三角形，∠ACB=∠DCE=90°,點A，D，E在同一直線上，CM為△DCE中DE邊上的高，連接BE．請判斷∠AEB的度數(shù)及線段CM，AE，BE之間的數(shù)量關(guān)系，并說明理由． 圖1-10-56 (3)解決問題 如圖1-10-57，在正方形ABCD中，CD=．若點P滿足PD=1,且∠BPD=90°，請直接寫出點A到BP的距離． 圖1-10-57 【解

11、】 (1)①60；②AD=BE. (2)∠AEB＝90°；AE=2CM+BE. 【理由】∵ △ACB和△DCE均為等腰直角三角形，∠ACB=∠DCE=90°, ∴ AC=BC,CD=CE. ∵ ∠ACB－∠DCB=∠DCE－∠DCB, 即∠ACD=∠BCE，∴ △ACD≌△BCE. ∴ AD=BE,∠BEC=∠ADC=135°. ∴ ∠AEB=∠BEC－∠CED=135°－45°=90°． 在等腰直角三角形DCE中，CM為斜邊DE上的高， ∴ CM=DM=ME,∴ DE=2CM. ∴ AE=DE+AD=2CM+BE. (3)或. 【提示】∵ PD=1，∠BPD=90°

12、, ∴ BP是以點D為圓心，以1為半徑的⊙D的切線，點P為切點． 第一種情況：如圖1-10-58，過點A作AP的垂線，交BP于點P′，過點A作AM⊥BP交BP于點M. 可證△APD≌△AP′B,PD=P′B=1. ∵ CD=,∴ BD=2,BP=, ∴ AM=PP′=(PB－BP′)=. 圖1-10-58 第二種情況如圖1-10-59，可得AM=PP′=(PB+BP′)=. 圖1-10-59 真題演練 1.如圖1-10-60，已知D是AC上一點，AB=DA，DE∥AB，∠B=∠DAE.求證：BC=AE. 圖1-10-60 【證明】 ∵ DE∥AB，∴ ∠CAB=∠ADE. 在△ABC與△DAE中， ∴ △ABC≌△DAE(ASA)，∴ BC=AE. 2.如圖1-10-61，已知點E，A，C在同一條直線上，AB∥CD,AB=CE,AC=CD.求證：BC＝ED. 圖1-10-61 【證明】 ∵ AB∥CD，∴ ∠BAC=∠ECD. 在△BAC和△ECD中， ∴ △BAC≌△ECD(SAS)，∴ CB=ED． 9