《新編高中數(shù)學(xué)北師大版選修22教案：第4章 拓展資料：用定積分求面積的兩個(gè)常用公式》由會員分享，可在線閱讀，更多相關(guān)《新編高中數(shù)學(xué)北師大版選修22教案：第4章 拓展資料：用定積分求面積的兩個(gè)常用公式（2頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。
1、新編數(shù)學(xué)北師大版精品資料
用定積分求面積的兩個(gè)常用公式
求平面圖形圍成的面積是定積分重要應(yīng)用之一，下面介紹求面積的兩個(gè)常用公式及其應(yīng)用．
一、兩個(gè)常用公式
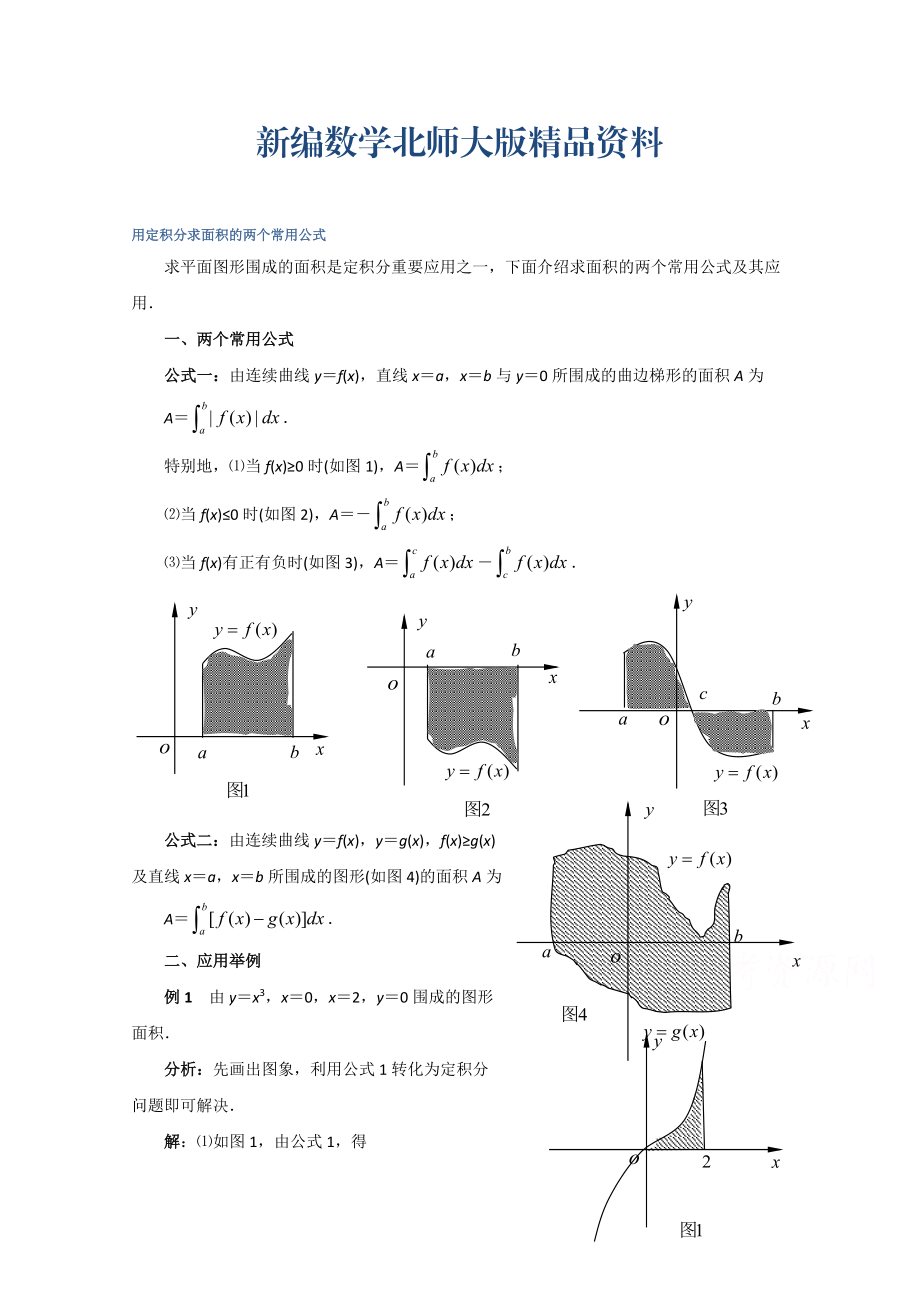
公式一：由連續(xù)曲線y＝f(x)，直線x＝a，x＝b與y＝0所圍成的曲邊梯形的面積A為
A＝．
特別地，⑴當(dāng)f(x)≥0時(shí)(如圖1)，A＝；
⑵當(dāng)f(x)≤0時(shí)(如圖2)，A＝－；
⑶當(dāng)f(x)有正有負(fù)時(shí)(如圖3)，A＝－．
公式二：由連續(xù)曲線y＝f(x)，y＝g(x)，f(x)≥g(x)及直線x＝a，x＝b所圍成的圖形(如圖4)的面積A為
A＝．
二、應(yīng)用舉例
例1 由y＝x3，x＝0，x＝2，y＝0圍成的圖形
2、面積．
分析：先畫出圖象，利用公式1轉(zhuǎn)化為定積分問題即可解決．
解：⑴如圖1，由公式1，得
S＝＝．
評注：注意定積分與利用定積分計(jì)算曲線圍成圖形的面積區(qū)別．定積分是一種積分和的極限，可為正，也可為負(fù)或零，而平面圖形的面積在一般意義上總為正．一般情況下，借助定積分分別求出每一部分曲邊梯形的面積，然后將它們加在一起．
例2 ⑴由曲線y＝x2，y2＝x所圍成圖形的面積．
⑵由y＝x2－1，y＝x，y＝在第一象限所圍成圖形的面積．
分析：先畫圖象找出范圍，利用公式2，用積分表示，再求積分．
解：⑴ 如圖2，所求面積為陰影部分．
解方程組，得交點(diǎn)(0，0)，(1，1)，由公式2，得
S＝＝．
⑵如圖3，解方程組和，
得x＝0，x＝1＋(負(fù)的舍去)，x＝4．
由公式2，得圖形面積
S＝＋
．
新編高中數(shù)學(xué)北師大版選修22教案：第4章 拓展資料：用定積分求面積的兩個(gè)常用公式
