《中考數(shù)學(xué)專題復(fù)習(xí) 壓軸題訓(xùn)練題2》由會(huì)員分享��,可在線閱讀��,更多相關(guān)《中考數(shù)學(xué)專題復(fù)習(xí) 壓軸題訓(xùn)練題2(3頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索���。
1、中考數(shù)學(xué)專題復(fù)習(xí) 壓軸題訓(xùn)練題2
為了沖刺中考數(shù)學(xué)140分�����,我拼了!
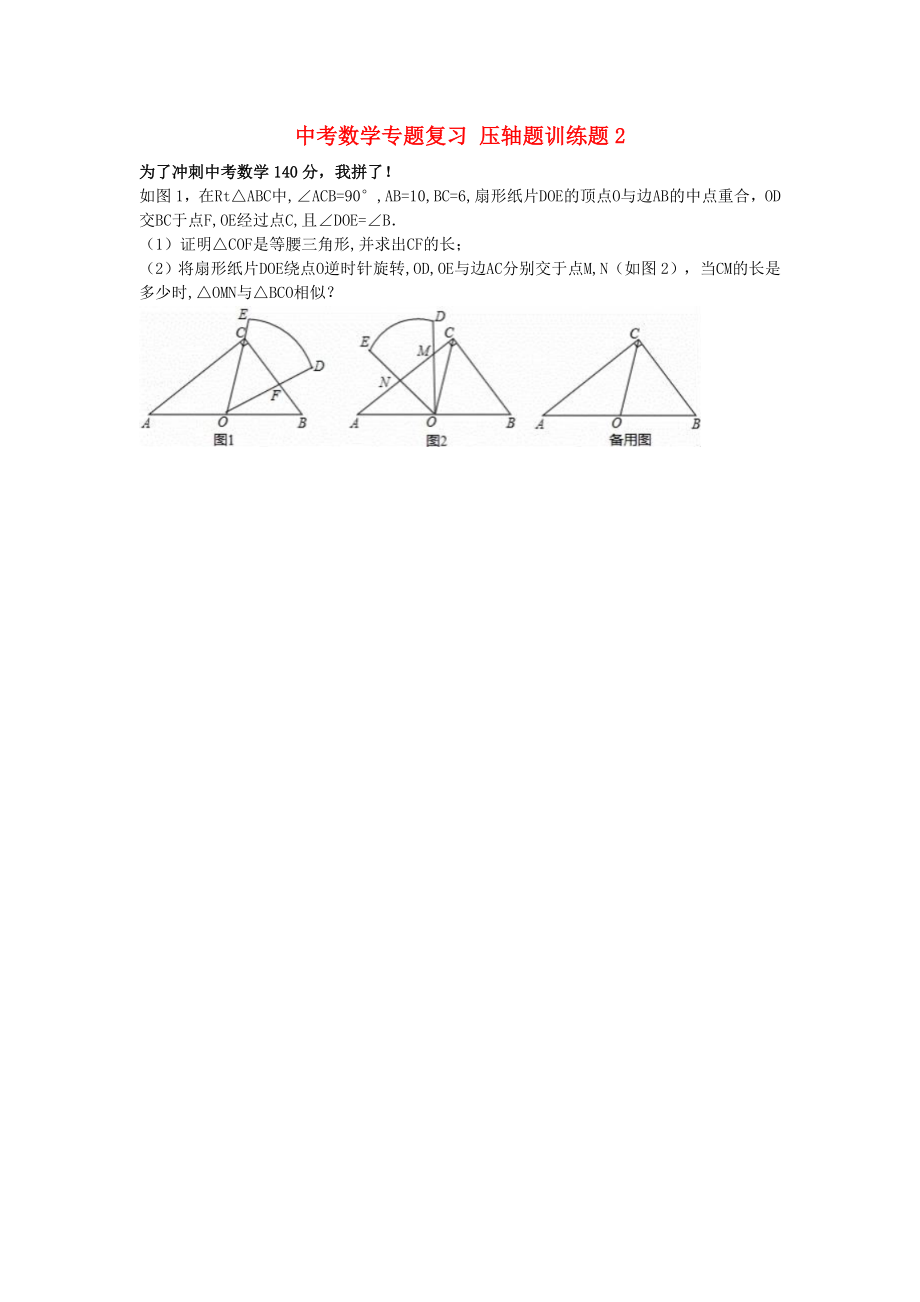
如圖1��,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,扇形紙片DOE的頂點(diǎn)O與邊AB的中點(diǎn)重合�,OD交BC于點(diǎn)F,OE經(jīng)過(guò)點(diǎn)C,且∠DOE=∠B.
(1)證明△COF是等腰三角形,并求出CF的長(zhǎng);
(2)將扇形紙片DOE繞點(diǎn)O逆時(shí)針旋轉(zhuǎn),OD,OE與邊AC分別交于點(diǎn)M,N(如圖2)��,當(dāng)CM的長(zhǎng)是多少時(shí),△OMN與△BCO相似��?
如圖��,已知拋物線的方程C1:
2�、 (m>0)與x軸交于點(diǎn)B、C���,與y軸交于點(diǎn)E��,且點(diǎn)B在點(diǎn)C的左側(cè).
(1)若拋物線C1過(guò)點(diǎn)M(2, 2)��,求實(shí)數(shù)m的值�����;
(2)在(1)的條件下�,求△BCE的面積;
(3)在(1)的條件下���,在拋物線的對(duì)稱軸上找一點(diǎn)H���,使得BH+EH最小,求出點(diǎn)H的坐標(biāo)�;
(4)在第四象限內(nèi),拋物線C1上是否存在點(diǎn)F���,使得以點(diǎn)B�、C����、F為頂點(diǎn)的三角形與△BCE相似���?若存在����,求m的值�;若不存在,請(qǐng)說(shuō)明理由.
解:(1)m=4………………………………2分
(2):B(-2,0)C(4
3�、,0)E(0,2)
………… …………5分
(3)如圖2��,拋物線的對(duì)稱軸是直線x=1�,當(dāng)H落在線段EC上時(shí)����,BH+EH最小.
設(shè)對(duì)稱軸與x軸的交點(diǎn)為P����,那么.
因此.解得.所以點(diǎn)H的坐標(biāo)為.…………………8分
(4)①如圖3,過(guò)點(diǎn)B作EC的平行線交拋物線于F�,過(guò)點(diǎn)F作FF′⊥x軸于F′.
由于∠BCE=∠FBC,所以當(dāng)����,即時(shí),△BCE∽△FBC.
設(shè)點(diǎn)F的坐標(biāo)為�,由,得.
解得x=m+2.所以F′(m+2, 0).
由�����,得.所以.
由����,得.
整理�,得0=16.此方程無(wú)解.………………10分
圖2 圖3 圖4
②如圖4�,作∠CBF=45°交拋物線于F,過(guò)點(diǎn)F作FF′⊥x軸于F′�����,
由于∠EBC=∠CBF��,所以��,即時(shí)�,△BCE∽△BFC.
在Rt△BFF′中,由FF′=BF′����,得.
解得x=2m.所以F′.所以BF′=2m+2,.
由�,得.解得.
綜合①、②����,符合題意的m為.…………………12分
 中考數(shù)學(xué)專題復(fù)習(xí) 壓軸題訓(xùn)練題2
中考數(shù)學(xué)專題復(fù)習(xí) 壓軸題訓(xùn)練題2