《結(jié)構(gòu)力學(xué)》第十四章結(jié)構(gòu)振動(dòng)與穩(wěn)定.ppt

《《結(jié)構(gòu)力學(xué)》第十四章結(jié)構(gòu)振動(dòng)與穩(wěn)定.ppt》由會(huì)員分享，可在線閱讀，更多相關(guān)《《結(jié)構(gòu)力學(xué)》第十四章結(jié)構(gòu)振動(dòng)與穩(wěn)定.ppt（39頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

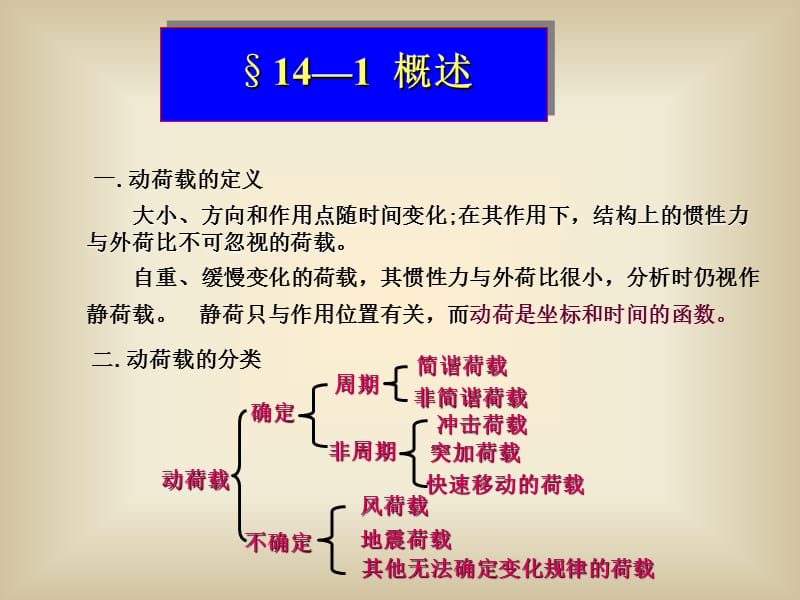
1、141 概述,一.動(dòng)荷載的定義,大小、方向和作用點(diǎn)隨時(shí)間變化;在其作用下，結(jié)構(gòu)上的慣性力 與外荷比不可忽視的荷載。,自重、緩慢變化的荷載，其慣性力與外荷比很小，分析時(shí)仍視作 靜荷載。 靜荷只與作用位置有關(guān)，而動(dòng)荷是坐標(biāo)和時(shí)間的函數(shù)。,二.動(dòng)荷載的分類,一. 自由度的定義,確定振動(dòng)過(guò)程中結(jié)構(gòu)中所有質(zhì)點(diǎn)位置所需的獨(dú)立參數(shù)的數(shù)目，稱作 結(jié)構(gòu)的振動(dòng)自由度。,142 結(jié)構(gòu)振動(dòng)的自由度,二. 自由度的確定,W=2,W=2,彈性支座不減少振動(dòng)自由度,為減少振動(dòng)自由度，梁與剛架不 計(jì)軸向變形。,,W=1,5),W=2,振動(dòng)自由度與質(zhì)點(diǎn)個(gè)數(shù)無(wú)關(guān)，但 不大于質(zhì)點(diǎn)個(gè)數(shù)的2倍。,W=2,W=1,W=1,W=13,振動(dòng)

2、自由度為1的結(jié)構(gòu)稱作單自由度結(jié)構(gòu)； 振動(dòng)自由度大于1的結(jié)構(gòu)稱作多自由度結(jié)構(gòu); 振動(dòng)自由度無(wú)限多的結(jié)構(gòu)稱為無(wú)限自由度結(jié)構(gòu)。,143 單自由度結(jié)構(gòu)的自由振動(dòng),一、不計(jì)阻尼的自由振動(dòng),自由振動(dòng)---由初位移、初速度引起的,在振動(dòng)中無(wú)動(dòng)荷載作用的振動(dòng)。,分析自由振動(dòng)的目的---確定體系的動(dòng)力特性：頻率、周期。,1.振動(dòng)微分方程及其解,阻尼---耗散能量的作用。,令,二階線性齊次常微分方程,2.振動(dòng)分析,單自由度結(jié)構(gòu)不計(jì)阻尼時(shí)的自由振動(dòng)是簡(jiǎn)諧振動(dòng).,自振周期,自振園頻率(自振頻率),3.自振頻率和周期的計(jì)算,利用計(jì)算公式,算例,例一.求圖示體系的自振頻率和周期.,解:,例二.求圖示體系的自振頻率和周期.

3、,解:,,例三.質(zhì)點(diǎn)重W,求體系的頻率和周期.,解:,2）.振動(dòng)分析,,,,,,,,,,,周期延長(zhǎng),計(jì)算頻率和周期可不計(jì)阻尼,例: 對(duì)圖示體系作自由振動(dòng)試驗(yàn).用鋼 絲繩將上端拉離平衡位置2cm,用 力16.4kN,將繩突然切斷,開始作 自由振動(dòng).經(jīng)4周期,用時(shí)2秒,振幅 降為1cm.求,1.阻尼比 2.剛度系數(shù) 3.無(wú)阻尼周期 4.重量 5.阻尼系數(shù),,振動(dòng)是衰減的,對(duì)數(shù)遞減量,利用此式,通過(guò)實(shí)驗(yàn)可確定 體系的阻尼比.上式也可寫成,6.若質(zhì)量增加800kg體系 的周期和阻尼比為多少,解:,1.阻尼比,2.剛度系數(shù),3.無(wú)阻尼周期,4.重量,5.阻尼系數(shù),6.若質(zhì)量增加800kg,體系的周

4、期和阻尼比 為多少,1.振動(dòng)微分方程及其解,二階線性非齊次常微分方程,一、不考慮阻尼,F ---荷載幅值,---干擾力頻率,振動(dòng)微分方程,或,通解,其中,設(shè),代入方程,可得,通解為,144 單自由度結(jié)構(gòu)在簡(jiǎn)諧荷載作用下的強(qiáng)迫振動(dòng),,,,,,1,1,單自由度結(jié)構(gòu)的位移動(dòng)力系數(shù)與內(nèi)力 動(dòng)力系數(shù)相同，統(tǒng)稱為動(dòng)力系數(shù)。,2.純強(qiáng)迫振動(dòng)分析,---荷載幅值作為靜荷載所引起的靜力位移,---位移動(dòng)力系數(shù),---最大動(dòng)力位移（振幅）,---頻比,若要使振幅降低,應(yīng)采取何種措施?,通過(guò)改變頻比可增加或減小振幅.,應(yīng)使頻比減小.,增加結(jié)構(gòu)自頻.,增加剛度、減小質(zhì)量.,應(yīng)使頻比增大.,減小結(jié)構(gòu)自頻.,減小剛度、增

5、大質(zhì)量.,例1 求圖示體系振幅和動(dòng)彎矩幅值圖，已知,3.動(dòng)位移、動(dòng)內(nèi)力幅值計(jì)算,計(jì)算步驟:,1）.計(jì)算荷載幅值作為靜荷載所引起的 位移、內(nèi)力；,2）.計(jì)算動(dòng)力系數(shù)；,3）.將得到的位移、內(nèi)力乘以動(dòng)力系數(shù) 即得動(dòng)位移幅值、動(dòng)內(nèi)力幅值。,解.,例2 求圖示梁中最大彎矩和跨中點(diǎn)最大位移 已知:,解.,重力引起的彎矩,重力引起的位移,振幅,動(dòng)彎矩幅值,跨中最大彎矩,跨中最大位移,動(dòng)荷載不作用于質(zhì)點(diǎn)時(shí)的計(jì)算,m,令,仍是位移動(dòng)力系數(shù),是內(nèi)力動(dòng)力系數(shù)嗎?,振動(dòng)微分方程,穩(wěn)態(tài)解,振幅,列幅值方程求內(nèi)力幅值,解:,例:求圖示體系振幅、動(dòng)彎矩幅值圖.已知,,解:,例:求圖示體系右端的質(zhì)點(diǎn)振幅,o,二.考慮阻尼

6、,1.振動(dòng)微分方程及其解,設(shè),或,通解,初位移、初速度引起的自由振動(dòng)分量,動(dòng)荷載激起的按結(jié)構(gòu)自振頻率振動(dòng)的分量,稱為伴生自由振動(dòng),純強(qiáng)迫振動(dòng),2.阻尼對(duì)振幅的影響,在平穩(wěn)階段,隨 增大而減小,阻尼在共振區(qū)內(nèi)影響顯著, 在共振區(qū)外可不計(jì)阻尼.,的最大值并不發(fā)生在,位移滯后于荷載,3.動(dòng)內(nèi)力、動(dòng)位移計(jì)算,除動(dòng)力系數(shù)計(jì)算式不同外， 其它過(guò)程與無(wú)阻尼類似。,例.圖示為塊式基礎(chǔ).機(jī)器與基礎(chǔ)的質(zhì)量為 ;地基豎向 剛度為 ;豎向振動(dòng)時(shí)的阻尼比為 機(jī)器轉(zhuǎn)速為N=800r/min,其偏心質(zhì)量引起的離心力為P=30kN.求豎向 振動(dòng)時(shí)的振幅。,解：,將荷載看成是連續(xù)作用的一系 列瞬時(shí)沖量，

7、求出每個(gè)瞬時(shí)沖 量引起的位移后將這些位移相 加即為動(dòng)荷載引起的位移。,一.瞬時(shí)沖量的反應(yīng),,,,,,,,,,,1.t=0 時(shí)作用瞬時(shí)沖量,m,,,2. 時(shí)刻作用瞬時(shí)沖量,145 單自由度結(jié)構(gòu)在任意荷載作用下的強(qiáng)迫振動(dòng),二.動(dòng)荷載的位移反應(yīng),---杜哈美積分,不計(jì)阻尼時(shí),若t=0 時(shí)結(jié)構(gòu)有初位移、初速度,不計(jì)阻尼時(shí),例.求突加荷載作用下的位移，開始時(shí)靜止，不計(jì)阻尼。,解：,動(dòng)力系數(shù)為 2,146 多自由度結(jié)構(gòu)的自由振動(dòng),自由振動(dòng)分析的目的是確定體系的動(dòng)力特性.可不計(jì)阻尼。,一.振動(dòng)微分方程及其解,或,振動(dòng)方程,,設(shè)方程的特解為,代入方程,得,,,---頻率方程,解頻率方程得 的兩個(gè)根,值小者記作

8、,,稱作第一頻率,也稱作基本頻率;,值大者記作,稱為第二頻率或高階頻率.,將 頻率代入振型方程,特解1,特解2,通解,二.頻率與振型,結(jié)構(gòu)按特解振動(dòng)時(shí)有如下特點(diǎn),1)各質(zhì)點(diǎn)同頻同步;,2)任意時(shí)刻,各質(zhì)點(diǎn)位移的比 值保持不變,定義:結(jié)構(gòu)上所有質(zhì)量按相同頻率作自由振動(dòng)時(shí) 的振動(dòng)形狀稱作結(jié)構(gòu)的主振型。,幾點(diǎn)說(shuō)明：,1.按振型作自由振動(dòng)時(shí)，各質(zhì)點(diǎn)的 速度的比值也為常數(shù)，且與位移 比值相同。,2.發(fā)生按振型的自由振動(dòng)是有條件的.,3.振型與頻率是結(jié)構(gòu)本身固有的屬性, 與外界因素?zé)o關(guān).,5。若已知柔度矩陣時(shí),6。求振型、頻率可列幅值方程.,振型方程,頻率方程,按振型振動(dòng)時(shí),振型可看作是結(jié)構(gòu)按振型振動(dòng)時(shí)， 慣性力幅值作為靜荷載所引起的靜位移,三.求頻率、振型例題,例一.求圖示體系的頻率、振型,解,令,對(duì)稱體系的振型分 成兩組:,一組為對(duì)稱振型,一組為反對(duì)稱振型,第二振型,解:,例二.求圖示體系的頻率、振型. 已知:,,,