《新版高考數(shù)學(xué)文二輪復(fù)習(xí) 課時(shí)鞏固過關(guān)練十二 Word版含解析》由會(huì)員分享�����,可在線閱讀���,更多相關(guān)《新版高考數(shù)學(xué)文二輪復(fù)習(xí) 課時(shí)鞏固過關(guān)練十二 Word版含解析(5頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1�、
1
2、 1
課時(shí)鞏固過關(guān)練(十二) 空間幾何體的三視圖��、表面積及體積
一��、選擇題
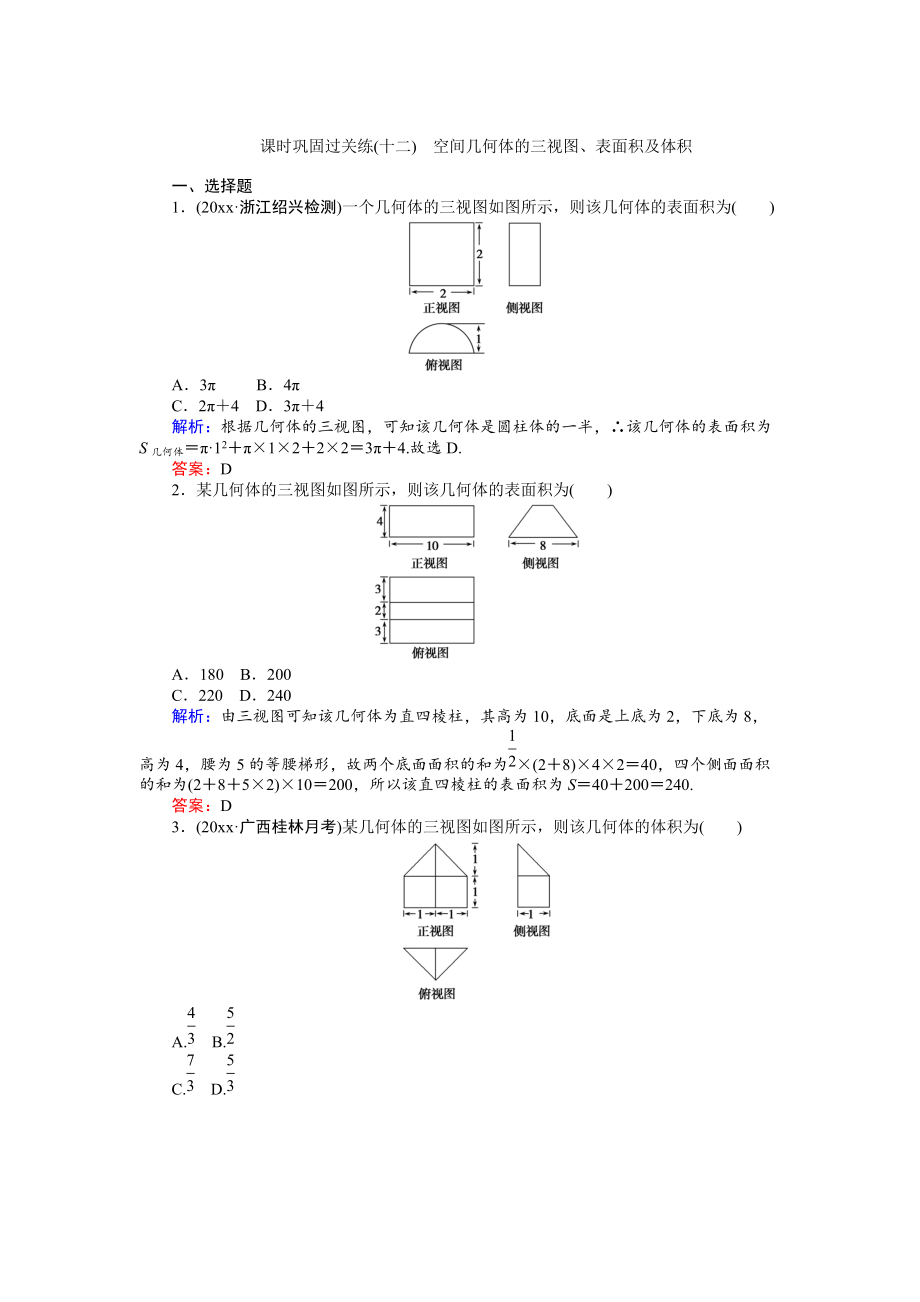
1.(20xx·浙江紹興檢測(cè))一個(gè)幾何體的三視圖如圖所示�����,則該幾何體的表面積為( )
A.3π B.4π
C.2π+4 D.3π+4
解析:根據(jù)幾何體的三視圖�,可知該幾何體是圓柱體的一半,∴該幾何體的表面積為S幾何體=π·12+π×1×2+2×2=3π+4
3���、.故選D.
答案:D
2.某幾何體的三視圖如圖所示�����,則該幾何體的表面積為( )
A.180 B.200
C.220 D.240
解析:由三視圖可知該幾何體為直四棱柱�,其高為10,底面是上底為2����,下底為8,高為4���,腰為5的等腰梯形����,故兩個(gè)底面面積的和為×(2+8)×4×2=40��,四個(gè)側(cè)面面積的和為(2+8+5×2)×10=200���,所以該直四棱柱的表面積為S=40+200=240.
答案:D
3.(20xx·廣西桂林月考)某幾何體的三視圖如圖所示����,則該幾何體的體積為( )
A. B.
C. D.
解析:該幾何體為三棱柱與三棱錐的組合體����,如下圖����,三棱柱的底
4���、面是等腰直角三角形�,其面積S=×1×2=1����,高為1,故其體積V1=1×1=1����;三棱錐的底面是等腰直角三角形��,其面積S=×1×2=1���,高為1�,故其體積V2=×1×1=.故該幾何體的體積V=V1+V2=��,故選A.
答案:A
4.(20xx·江西吉安一中期中)某幾何體的三視圖如圖所示�,則該幾何體中,面積最大的側(cè)面的面積為( )
A. B.
C. D.3
解析:由三視圖可知,幾何體的直觀圖如圖所示��,平面AED⊥平面BCDE���,四棱錐A-BCDE的高為1����,四邊形BCDE是邊長(zhǎng)為1的正方形��,則S△AED=×1×1=����,S△ABC=S△ABE=×1×=,S△ACD=×1×=����,故選B.
5、答案:B
5.(20xx·遼寧沈陽(yáng)二中期中)某幾何體的三視圖如圖所示���,則這個(gè)幾何體的體積為( )
A.4 B.
C. D.8
解析:由三視圖知該幾何體為四棱錐與三棱錐的組合體���,其直觀圖如圖:其中SC⊥平面ABCD,AB⊥平面BCSE����,SC=4����,BE=2�,四邊形ABCD是邊長(zhǎng)為2的正方形,∴幾何體的體積V=V四棱錐S-ABCD+V三棱錐A-BSE=×22×4+××2×2×2=+=.故選B.
答案:B
6.(20xx·北京昌平期末抽測(cè))某三棱錐的三視圖如圖所示�,則該三棱錐四個(gè)面的面積中最大的是( )
A. B.3
C. D.3
解析:該幾何體的底面面
6、積為×3×1=�����,側(cè)面面積分別為×2×=���,××2=����,×3×=.其中最大面積為.
答案:C
7.(20xx·湖北一聯(lián))如圖是一個(gè)空間幾何體的三視圖���,則該幾何體的外接球的表面積為( )
A.8π B.16π
C.32π D.64π
解析:由三視圖知該幾何體是三棱錐,且底面是等腰直角三角形����,三棱錐的高是2,底面的直角邊長(zhǎng)為,斜邊為2����,則三棱錐的外接球是對(duì)應(yīng)直三棱柱的外接球,設(shè)幾何體外接球的半徑為R��,因底面是等腰直角三角形�����,則底面外接圓的半徑為1����,又高為2,所以R2=1+1=2�����,故外接球的表面積是4πR2=8π�,故選A.
答案:A
8.(20xx·江西贛州三考)某幾何體的三視圖如
7、圖所示�,當(dāng)xy最大時(shí),該幾何體的體積為( )
A.2 B.3
C.4 D.6
解析:由三視圖得幾何體為三棱錐��,其直觀圖如圖.由題意得x2+y2=52+()2=32��,∵2xy≤x2+y2=32,∴xy≤16.當(dāng)且僅當(dāng)x=y(tǒng)=4時(shí)取等號(hào).此時(shí)AB==3.幾何體的體積V=××3×4×=2.故選A.
答案:A
9.(20xx·河北衡水二中期中)已知四面體P-ABC的外接球的球心O在AB上����,且PO⊥平面ABC,2AC=AB,若四面體P-ABC的體積為����,則該球的體積為( )
A.π B.2π
C.2π D.4π
解析:設(shè)該球的半徑為R,則AB=2R�����,2AC=AB
8���、=×2R���,所以AC=R,由于AB是球的直徑�,所以△ABC在大圓所在平面內(nèi)且有AC⊥BC.在Rt△ABC中,由勾股定理�����,得BC2=AB2-AC2=R2���,所以Rt△ABC的面積S=BC·AC=R2.又PO⊥平面ABC�����,且PO=R�,四面體P-ABC的體積為���,所以VP-ABC=×R×R2=��,即R3=9����,R3=3����,所以球的體積V球=πR3=×π×3=4π.故選D.
答案:D
10.(20xx·河南模擬)已知三棱錐O-ABC,A�,B,C三點(diǎn)均在球心為O的球表面上�,AB=BC=1,∠ABC=120°���,三棱錐O-ABC的體積為��,則球O的表面積是( )
A.544π B.16π
C.π D.
9�����、64π
解析:三棱錐O-ABC���,A���、B、C三點(diǎn)均在球心O的表面上���,且AB=BC=1��,
∠ABC=120°����,AC=�����,
∴S△ABC=×1×1×sin120°=�����,
∵三棱錐O-ABC的體積為,
△ABC的外接圓的圓心為G�����,
∴OG⊥⊙G���,
外接圓的半徑為:GA==1,
∴S△ABC·OG=��,
即×OG=���,OG=����,
球的半徑為:=4.
球的表面積:4π42=64π.
故選D.
答案:D
二�����、填空題
11.一個(gè)幾何體的三視圖如圖所示�����,其中正視圖是等邊三角形���,俯視圖是半圓.現(xiàn)有一只螞蟻從點(diǎn)A出發(fā)沿該幾何體的側(cè)面環(huán)繞一周回到A點(diǎn)�����,則螞蟻所經(jīng)過路程的最小值為__________.
解析:由題目所給三視圖可得�,該幾何體為圓錐的一半,側(cè)面展開圖是一個(gè)扇形和一個(gè)等邊三角形如圖����,扇形的半徑為2,弧長(zhǎng)為π�����,所以圓心角為����,因?yàn)橐粋€(gè)螞蟻從點(diǎn)A出發(fā)沿該幾何體的側(cè)面環(huán)繞一周回到A點(diǎn),連接AA′�����,則AA′為螞蟻所經(jīng)過的最短路徑.所以螞蟻所經(jīng)過路程的最小值為
=+.故答案為+.
答案:+
 新版高考數(shù)學(xué)文二輪復(fù)習(xí) 課時(shí)鞏固過關(guān)練十二 Word版含解析
新版高考數(shù)學(xué)文二輪復(fù)習(xí) 課時(shí)鞏固過關(guān)練十二 Word版含解析