《(安徽專用)2013年高考數(shù)學(xué)總復(fù)習(xí) 第三章第8課時(shí) 正弦定理和余弦定理的應(yīng)用舉例隨堂檢測(cè)(含解析)》由會(huì)員分享���,可在線閱讀�,更多相關(guān)《(安徽專用)2013年高考數(shù)學(xué)總復(fù)習(xí) 第三章第8課時(shí) 正弦定理和余弦定理的應(yīng)用舉例隨堂檢測(cè)(含解析)(2頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索��。
1��、
第三章第8課時(shí) 正弦定理和余弦定理的應(yīng)用舉例 隨堂檢測(cè)(含答案解析)
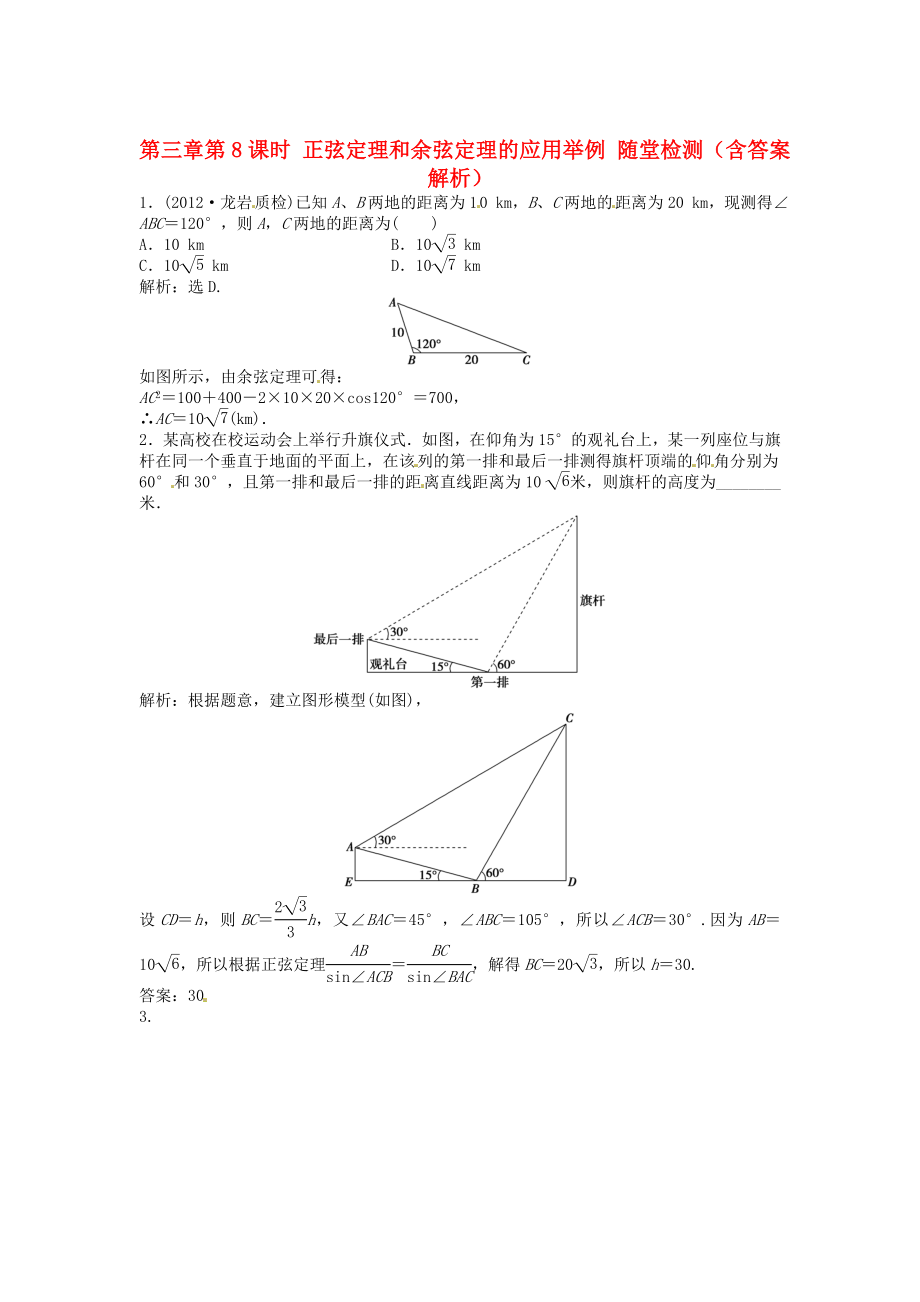
1.(2012·龍巖質(zhì)檢)已知A��、B兩地的距離為10 km��,B�����、C兩地的距離為20 km����,現(xiàn)測(cè)得∠ABC=120°��,則A���,C兩地的距離為( )
A.10 km B.10 km
C.10 km D.10 km
解析:選D.
如圖所示,由余弦定理可得:
AC2=100+400-2×10×20×cos120°=700����,
∴AC=10(km).
2.某高校在校運(yùn)動(dòng)會(huì)上舉行升旗儀式.如圖,在仰角為15°的觀禮臺(tái)上��,某一列座位與旗桿在同一個(gè)垂直于地面的平面上��,在該列的第一排和最后一排測(cè)得
2�����、旗桿頂端的仰角分別為60°和30°��,且第一排和最后一排的距離直線距離為10米���,則旗桿的高度為_(kāi)_______米.
解析:根據(jù)題意,建立圖形模型(如圖)��,
設(shè)CD=h,則BC=h��,又∠BAC=45°�,∠ABC=105°,所以∠ACB=30°.因?yàn)锳B=10����,所以根據(jù)正弦定理=,解得BC=20��,所以h=30.
答案:30
3.
如圖��,漁船甲位于島嶼A的南偏西60°方向的B處���,且與島嶼A相距12海里����,漁船乙以10海里/小時(shí)的速度從島嶼A出發(fā)沿正北方向航行���,若漁船甲同時(shí)從B處出發(fā)沿北偏東α的方向追趕漁船乙��,剛好用2小時(shí)追上.
(1)求漁船甲的速度�;
(2)求sinα的值.
解:(1)依題意知���,∠BAC=120°�,AB=12,AC=10×2=20���,∠BCA=α.
在△ABC中�,由余弦定理����,得
BC2=AB2+AC2-2AB·AC·cos∠BAC
=122+202-2×12×20×cos120°=784.
解得BC=28.
所以漁船甲的速度為=14海里/小時(shí).
(2)在△ABC中,因?yàn)锳B=12��,∠BAC=120°�,BC=28,∠BCA=α�,由正弦定理,得=���,
即sinα===.
 (安徽專用)2013年高考數(shù)學(xué)總復(fù)習(xí) 第三章第8課時(shí) 正弦定理和余弦定理的應(yīng)用舉例隨堂檢測(cè)(含解析)
(安徽專用)2013年高考數(shù)學(xué)總復(fù)習(xí) 第三章第8課時(shí) 正弦定理和余弦定理的應(yīng)用舉例隨堂檢測(cè)(含解析)